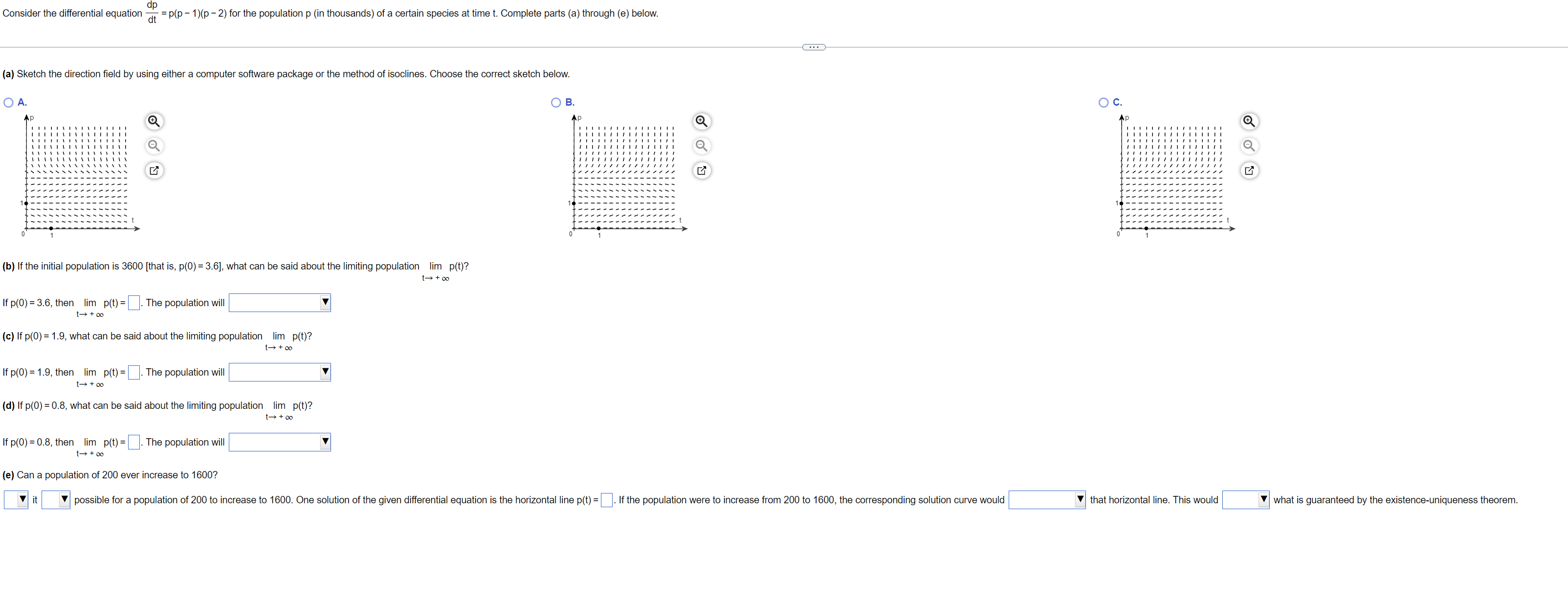
Consider the differential equation - = p(p - 1)(p -2) for the population p (in thousands) of a certain species at time t. Complete parts (a) through (e) below. (a) Sketch the direction field by using either a computer software package or the method of isoclines. Choose the correct sketch below. O A. O B. O C. b) If the initial population is 3600 [that is, p(0) = 3.6], what can be said about the limiting population lim p(t)? 1+ 00 If p(0) = 3.6, then lim p(t) = . The population will 1 - + 00 (c) If p(0) = 1.9, what can be said about the limiting population lim p(t)? 1 + 00 If p(0) = 1.9, then lim p(t) = . The population will 1 + 00 (d) If p(0) =0.8, what can be said about the limiting population lim p(t)? 1+ 00 If p(0) = 0.8, then lim p(t) = . The population will 1+ + 00 (e) Can a population of 200 ever increase to 1600? possible for a population of 200 to increase to 1600. One solution of the given differential equation is the horizontal line p(t) = ]. If the population were to increase from 200 to 1600, the corresponding solution curve would that horizontal line. This would what is guaranteed by the existence-uniqueness theorem