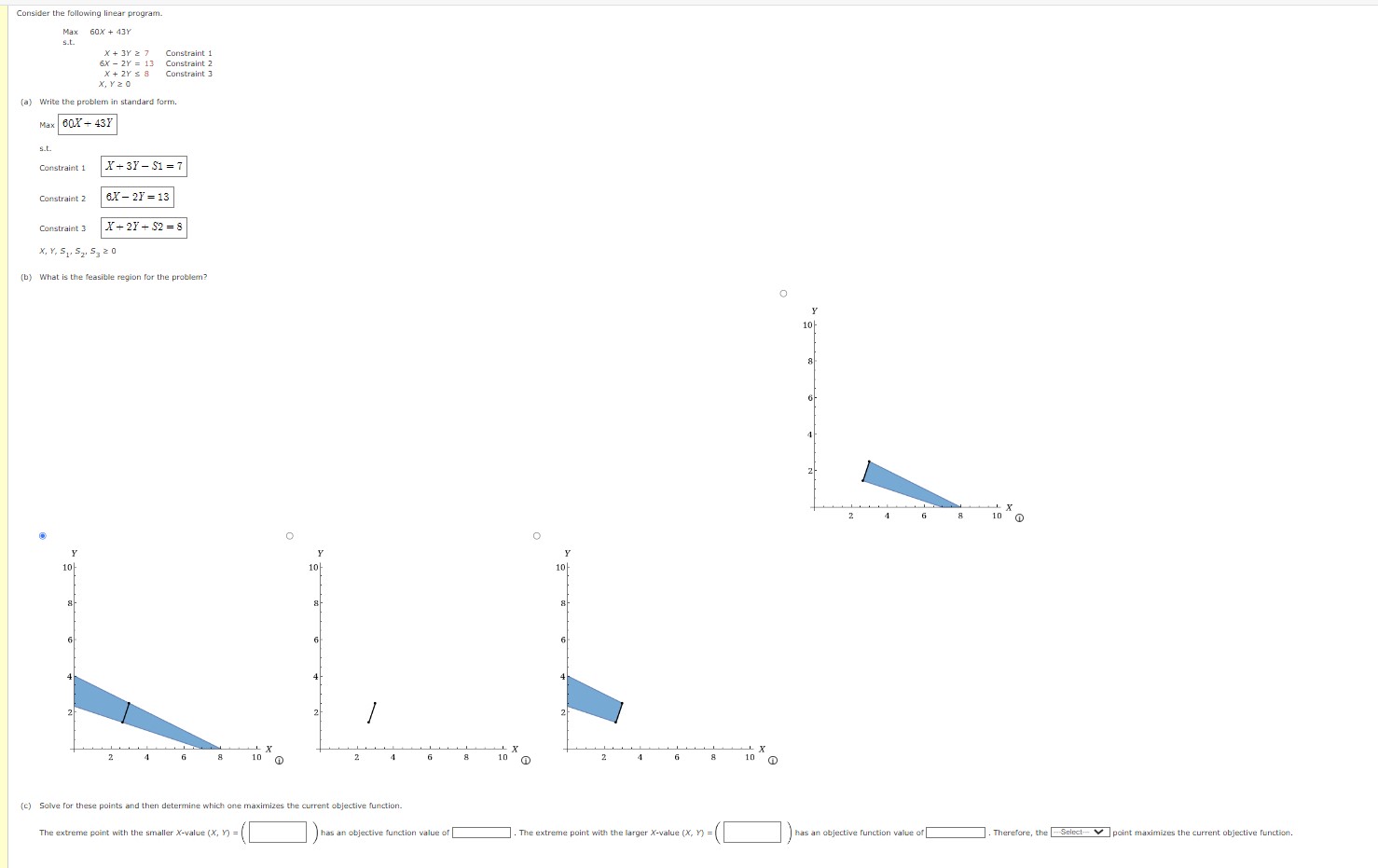
Consider the following linear program. Max 60X + 43Y s.t. X + 3Y 2 7 Constraint 1 6X - 2Y = 13 Constraint 2 X + 2Y s a Constraint 3 X, Y20 (a) Write the problem in standard form. Max 60X + 43Y s.t. Constraint 1 X + 3Y - S1 =7 Constraint 2 BY - 2Y =13 Constraint 3 X+ 2Y + $2 = 8 X, Y, 51. 52. 53 2 0 (b) What is the feasible region for the problem? O 10+ N 10 0 O O 2 10 10 2 10 0 (c) Solve for these points and then determine which one maximizes the current objective function. The extreme point with the smaller X-value (x, Y) = ( has an objective function value of . The extreme point with the larger X-value (x, v) =(] ) has an objective function value of . Therefore, the Select- point maximizes the current objective function