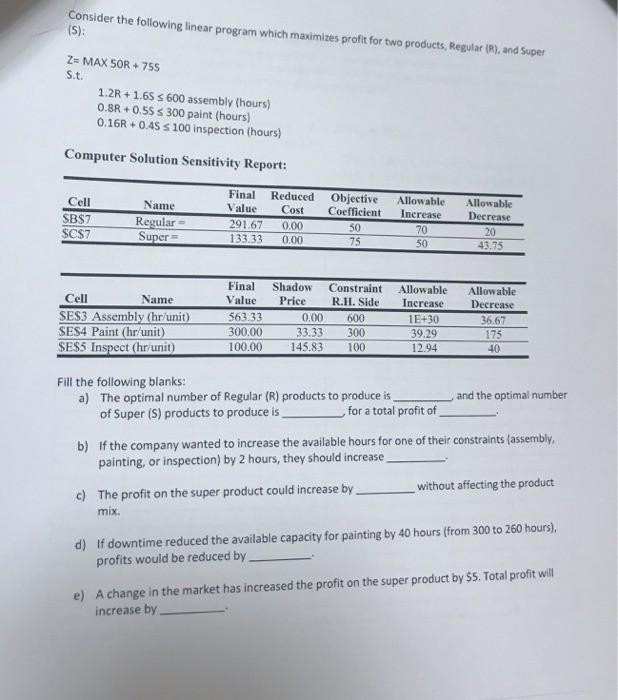
Consider the following linear program which maximizes profit for two products, Regular (R), and Super (s): Z= MAX 5OR + 755 St. 1.2R+1.65 600 assembly (hours) 0.8R+0.55 S 300 paint (hours) 0.16R+0.45 S 100 inspection (hours) Computer Solution Sensitivity Report: Cell SB$7 SCS7 Name Regular Super Final Value 291.67 133.33 Reduced Cost 0.00 0.00 Objective Coefficient 50 75 Allowable Increase 70 50 Allowable Decrease 20 43.75 Cell Name SES3 Assembly (hr/unit) SES4 Paint (hr/unit) $E$5 Inspect (hr unit) Final Value 563.33 300.00 100.00 Shadow Constraint Price R.H. Side 0.00 600 33.33 300 145.83 100 Allowable Increase 1E+30 39.29 12.94 Allowable Decrease 36.67 175 40 Fill the following blanks: a) The optimal number of Regular (R) products to produce is and the optimal number of Super (s) products to produce is for a total profit of b) If the company wanted to increase the available hours for one of their constraints (assembly, painting, or inspection) by 2 hours, they should increase c) The profit on the super product could increase by without affecting the product mix d) If downtime reduced the available capacity for painting by 40 hours (from 300 to 260 hours). profits would be reduced by e) A change in the market has increased the profit on the super product by $5. Total profit will increase by