Question: . Consider the following model for population growth with constant harvesting dy dt = y(1 y) - H where y(t) is the population in


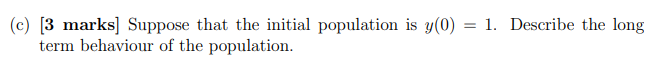
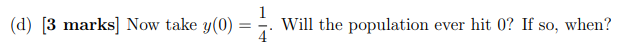
![[2 marks] Suppose that y(0) = . What is the rate of](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/05/663b373d08755_796663b373cdb6ef.jpg)
. Consider the following model for population growth with constant harvesting dy dt = y(1 y) - H where y(t) is the population in hundreds, t is time in months, and H is the harvesting term. For the entirety of this problem take H 1 1 4 (a) [2 marks] Suppose that y(0) = . What is the rate of change of the population at time t=0? Explain in a sentence what this implies about the population for all time. (b) [5 marks] Demonstrate that 1 y(t)= = t+C is a solution to our differential equation with H 4 (c) [3 marks] Suppose that the initial population is y(0) = 1. Describe the long term behaviour of the population. 1 (d) [3 marks] Now take y(0) = Will the population ever hit 0? If so, when? (e) [2 marks] Explain the difference in the fate of the population in parts (c) and (d) above. Why would we expect this difference from the start?
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


