Consider the following neural network with two binary inputs, x1 and x2. The inputs can assume a value of either 1 or +1. The output is likewise binary, with possible values of again 1 and +1.

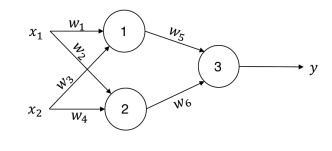
In this network, the perceptrons 1 and 2 implement the identity activation function, i.e., their outputs are the weighted sum of inputs. The perceptron 3 implements the sign activation function, i.e., the output is 1 if the weighted sum of inputs is negative and +1 otherwise. None of the perceptrons have a bias term. We will train this network to classify inputs into classes with labels +1 or 1. Consider the following training set:

Is it possible to train this network to have a zero classification error? If so, find an optimal (w1, w2, w3, w4, w5, w6). You can use any method that you want. The details of the algorithm is not wanted, just write down an optimal solution. If zero error is not possible, explain why not.

\begin{tabular}{ccc} \hlinex1 & x2 & y \\ \hline+1 & +1 & 1 \\ +1 & 1 & +1 \\ 1 & +1 & +1 \\ 1 & 1 & 1 \\ \hline \end{tabular}