Part B: Nonlinear Decision Boundary $(25$ points$)$

The XOR function $("$Exclusive OR$")$ is a digital logic operation on two binary inputs, $x_1$ and $x_2.$ The truth

table and the scatter plot for the four possible combinations of $(x_1,x_2)$ are shown below.

As we discussed in class, a single$-$layer Perceptron is insufficient to classify the XOR data points because

it can only create linear decision boundaries. To address this, consider a two$-$layer MLP with the

following activation functions:

For hidden layer, $f^{[1]}(z)=$ sigmoid; for output layer, $f^{[2]}(z)=$ sigmoid.

Given the specified weights and biases for this MLP$,$ please complete the following tasks.

$($a$)$ Forward Propagation: Compute the outputs of the two neurons in the hidden layer $($denoted as

$a_1^{[1]}$ and $a_2^{[1]})$ and the final output of the MLP $($denoted as $a^{[2]}$ or hat$(y)),$ for all four input

combinations of $(x_1,x_2).$ After completing the calculations, fill in the three tables provided

below with your results. $\backslash$table$[[$Neuron $1,$Neuron $2,$Output Neuron$],[$x$\_(1),$x$\_(2),$a$\_(1)^([1]),$x$\_(1),$x$\_(2),$a$\_(2)^([1]),$a$\_(1)^([1]),$a$\_(2)^([1]),$hat$($y$)],[0,0,,0,0,,,,],[0,1,,0,1,,,,],[1,0,,1,0,,,,],[1,1,,1,1,,,,]]$Problem $2$: Deriving the Decision Boundaries $(40$ points$)$

The decision boundary in a neural network refers to the surface that separates different classes in the

dataset. A neural network learns this boundary by adjusting its weights and biases during training.

Part A: Linear Decision Boundary $(15$ points$)$

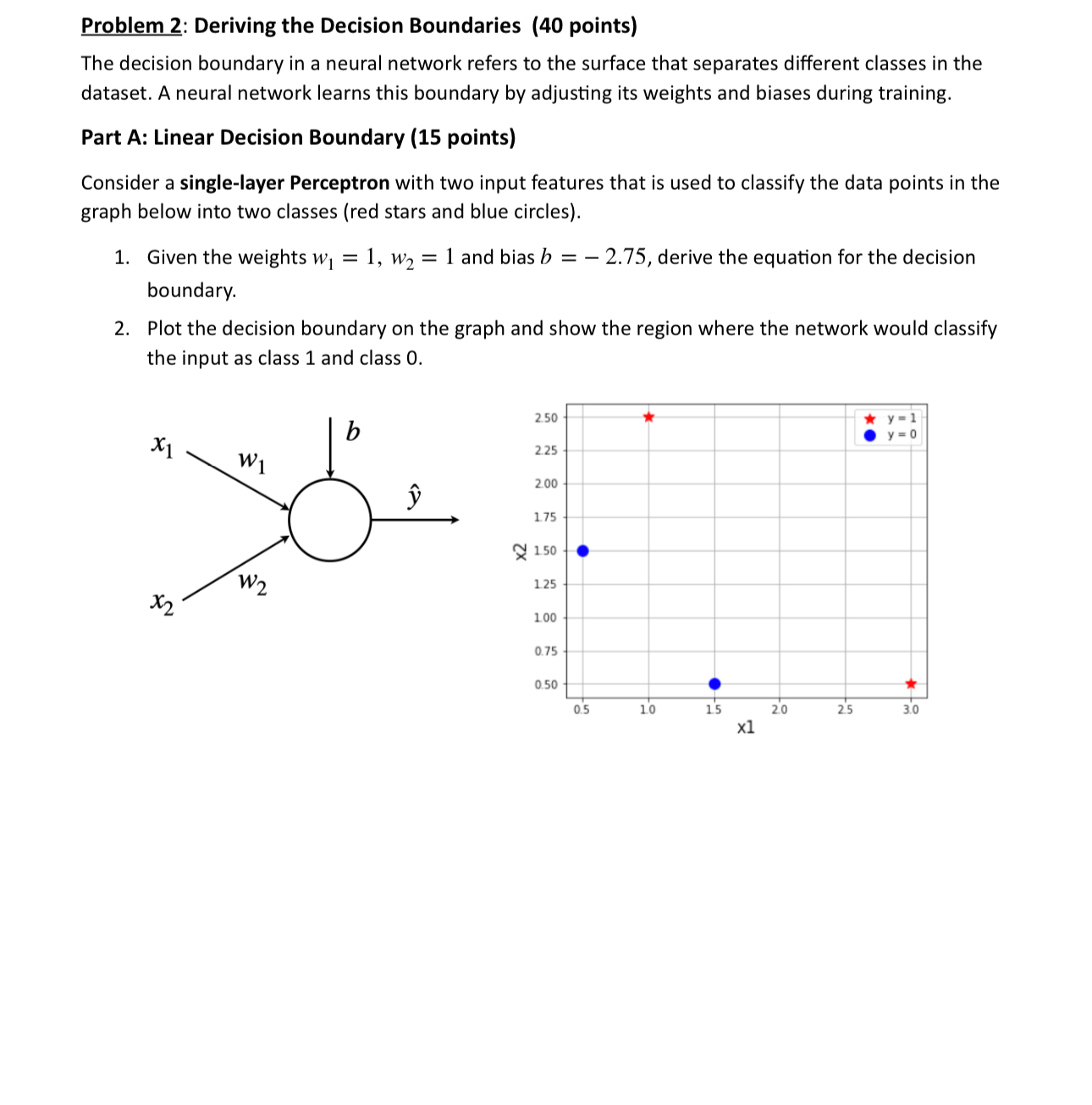
Consider a single$-$layer Perceptron with two input features that is used to classify the data points in the

graph below into two classes $($red stars and blue circles$).$

Given the weights $w_1=1,w_2=1$ and bias $b=-2\mathrm{.}75,$ derive the equation for the decision

boundary.

Plot the decision boundary on the graph and show the region where the network would classify

the input as class $1$ and class $0.$