Question: Consider the following queueing system. Customers arrive in pairs according to a Poisson process with rate ? = 1 customer pair/minute. There is one server
Consider the following queueing system. Customers arrive in pairs according to a
Poisson process with rate ? = 1 customer pair/minute. There is one server and room
for two customers to wait in line. Service times are exponential with mean 30 seconds.
If there is not room for both arriving customers, they both leave. (a) Describe the system
in a rate diagram and find the stationary distribution. (b) Now suppose that pairs may
split up. If there is not room for both, then with probability 1
2
they both leave and with
probability 1
2
one stays and the other leaves. Do (a) again under these assumptions.
46 Customer groups arrive to a service station according to a Poisson process with rate ?
groups/minute. With probability p, such a group consists of a single individual, and with
probability 1 ? p, it consists of a pair. There is a single server and room for two to wait
in line. Service times are exponential with rate . If a pair arrives and they cannot both
join, they both leave. (a) Give the state space and describe the system in a rate diagram.
(b) Suppose ? = and p =
1
2
. Find the stationary distribution (?0, ?1, ?2, ?3).
47 Phone calls arrive to a company according to two independent Poisson processes, one of
female callers with rate 2 and one of male callers with rate 1 (calls/minute). There is one
server and room for one to wait in line. If the server is busy, a female caller stays to wait
in line with probability 0.8; a male caller, with probability 0.5. Service times are i.i.d.
exponential with mean length 2 minutes. Let the state be the number of customers in the
system. (a) Describe the system in a rate diagram and find the stationary distribution.
(b) What proportion of callers are lost?
48 Consider an M/M/1 queue with arrival rate ? and service rate and where an arriving
customer who finds k individuals in the system joins with probability 1/(k + 1). When
does a stationary distribution exist and what is it?
49 Reneging. Consider an M/M/1 queue with arrival rate ? and service rate , where a
customer who is waiting in line reneges and leaves the line after a time that is exp(?)
(unless service has started), independent of the queue length. Describe this system in a
rate diagram and state the generator.
50 Consider an M/M/1 queue in equilibrium and let W be the waiting time of an arriving
customer. Find the cdf of W. What type of distribution is this? Hint: First find
P(W = 0), and then compute P(W > x) by conditioning on the number of customers
in the system.
51 Consider an M/M/1 queue in equilibrium and let T be the total time an arriving
customer spends in the system. Find the distribution of T (condition on the number of
customers in the system at arrival).
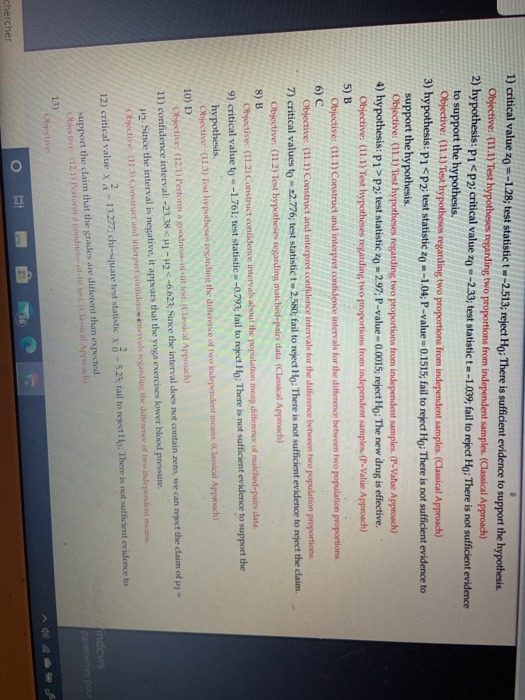


1) critical value zo =-1.28; test statistic t =-2.513; reject Ho; There is sufficient evidence to support the hypothesis. Objective: (11.1) Test hypotheses regarding two proportions from independent samples. (Classical Approach) 2) hypothesis: p1
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


