Consider the following two random variables: X has a (continuous) uniform density on (-2, 2), while Y is a discrete random variable defined by ( -2, 2 ; 1/2, 1/2 ).

Calculate the expected value of X: , and the expected value of Y: .

Calculate the variance of X (two decimals): , and the variance of Y: .

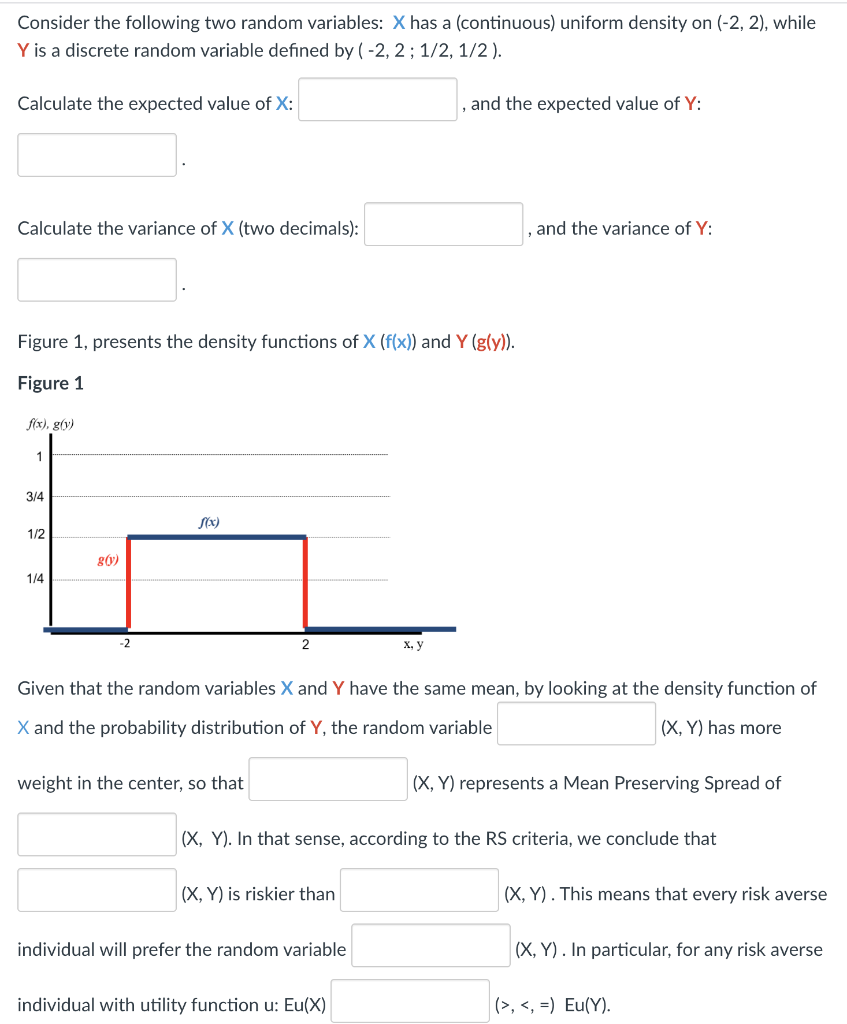
Figure 1, presents the density functions of X (f(x)) and Y (g(y)).

Figure 1

Given that the random variables X and Y have the same mean, by looking at the density function of X and the probability distribution of Y, the random variable (X, Y) has more weight in the center, so that (X, Y) represents a Mean Preserving Spread of (X, Y). In that sense, according to the RS criteria, we conclude that (X, Y) is riskier than (X, Y) . This means that every risk averse individual will prefer the random variable (X, Y) . In particular, for any risk averse individual with utility function u: Eu(X) (>, Consider the following two random variables: X has a continuous) uniform density on (-2, 2), while Y is a discrete random variable defined by (-2, 2; 1/2, 1/2). Calculate the expected value of X: and the expected value of Y: Calculate the variance of X (two decimals): and the variance of Y: Figure 1, presents the density functions of X (f(x)) and Y (gly)). Figure 1 f(x), g(1) 1 3/4 f(x) 1/2 80 1/4 -2 Given that the random variables X and Y have the same mean, by looking at the density function of X and the probability distribution of Y, the random variable (X, Y) has more weight in the center, so that (X, Y) represents a Mean Preserving Spread of (X, Y). In that sense, according to the RS criteria, we conclude that (X,Y) is riskier than (X,Y). This means that every risk averse individual will prefer the random variable (X, Y). In particular, for any risk averse individual with utility function u: Eu(X) (>,,