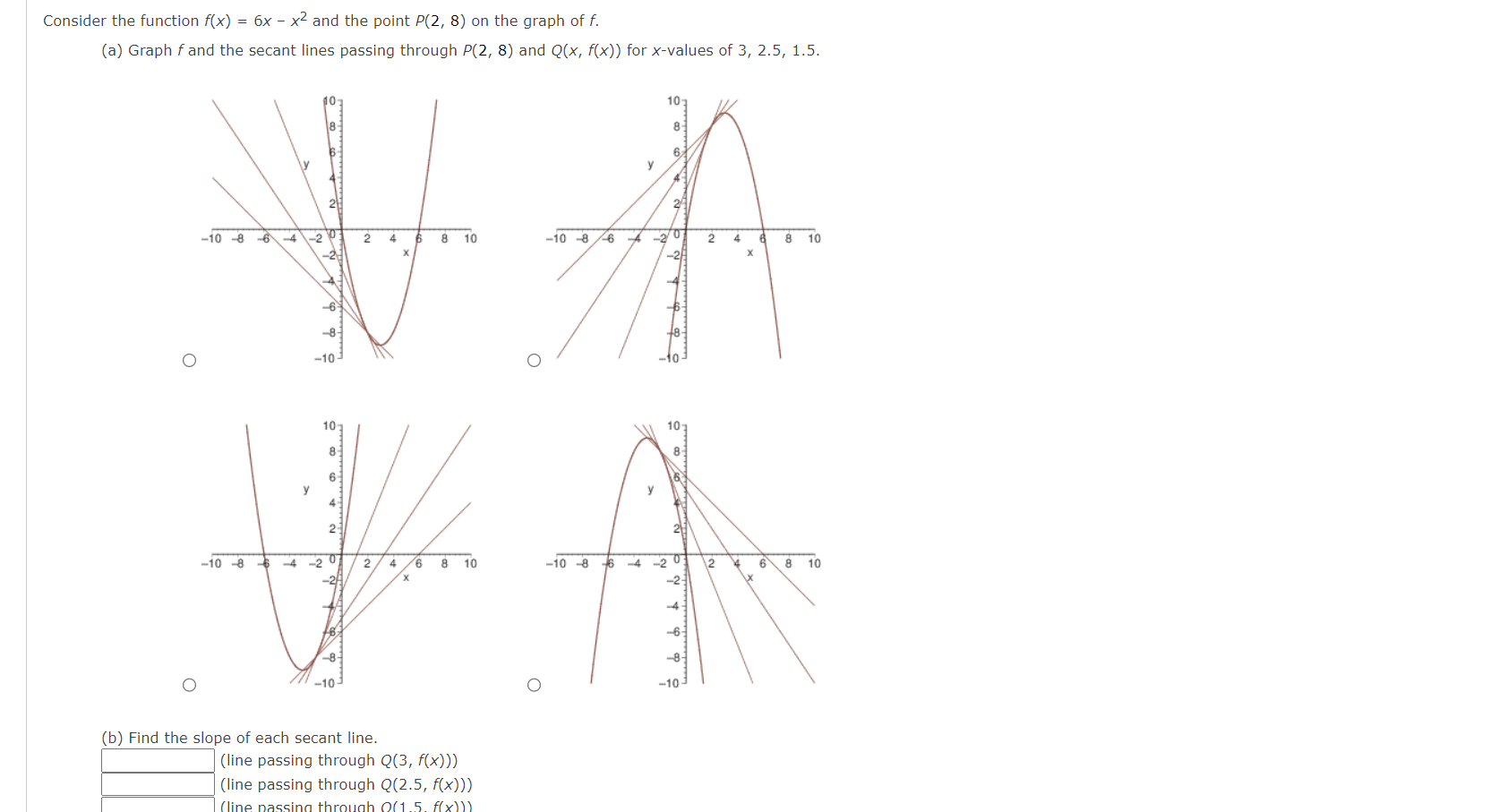
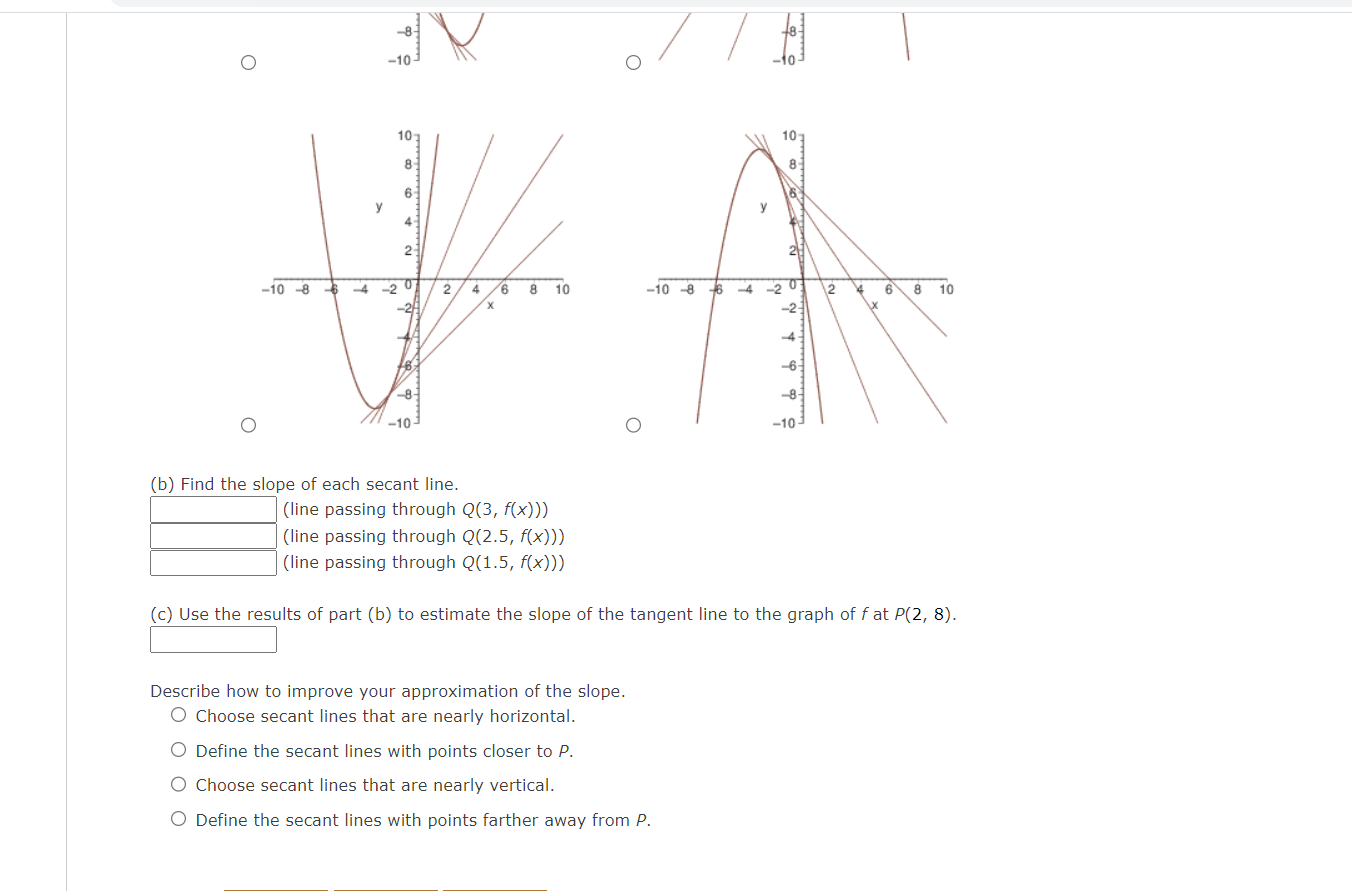
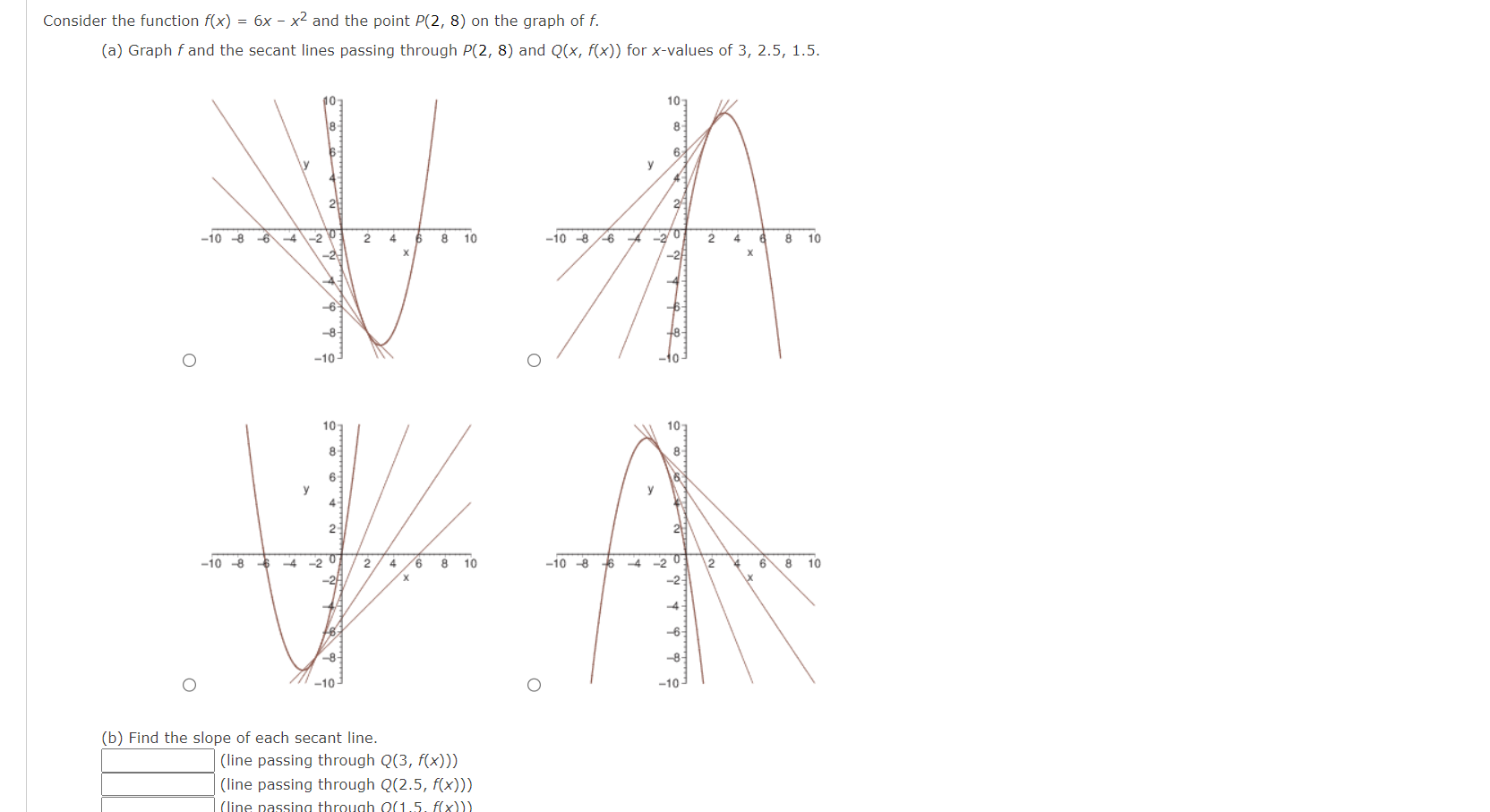
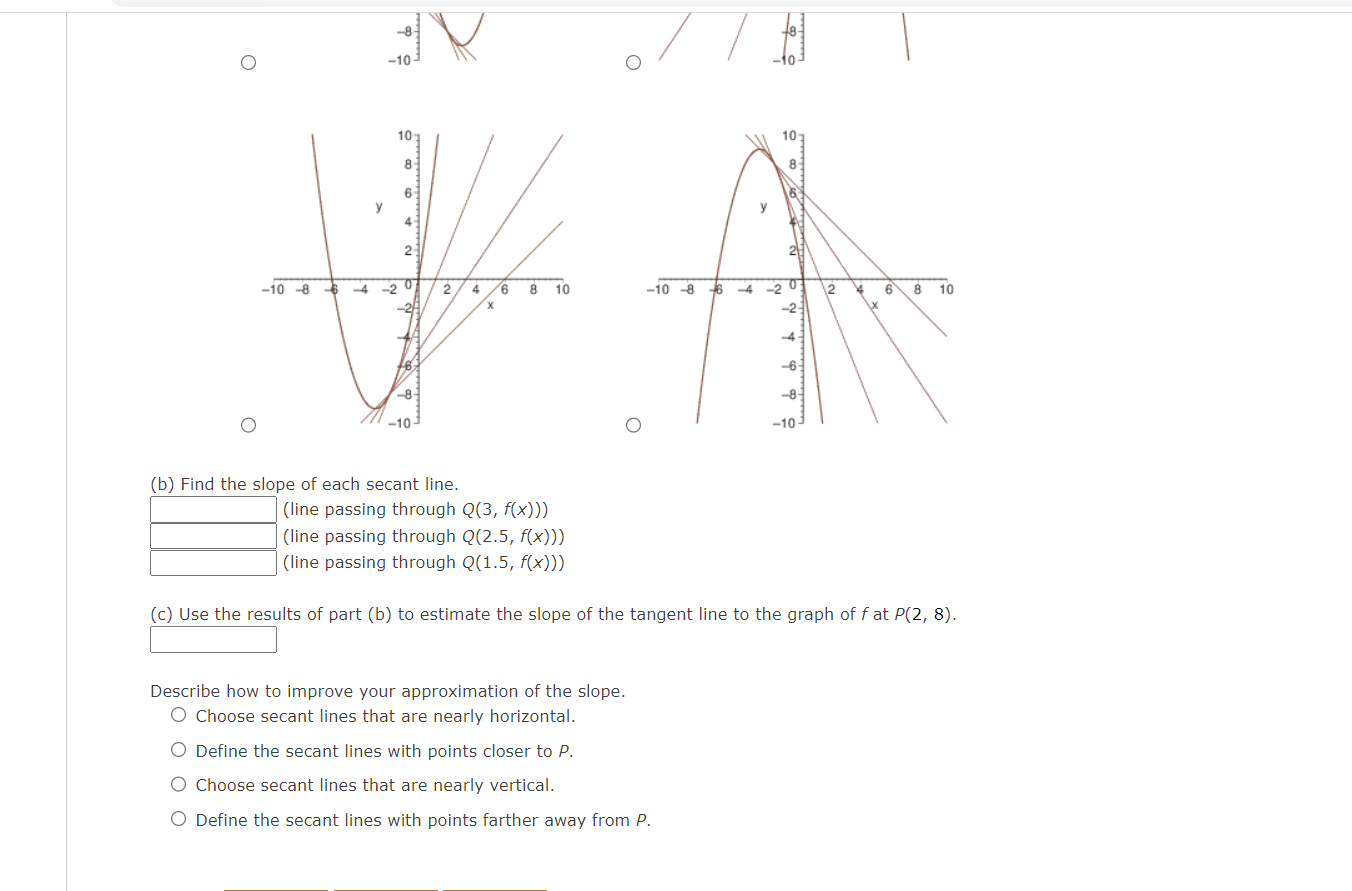
Consider the function f(x) = 6x - x2 and the point P(2, 8) on the graph of f. (a) Graph f and the secant lines passing through P(2, 8) and Q(x, f(x)) for x-values of 3, 2.5, 1.5. 23 -10 8 6 4 -2 2 8 10 -10 -8 6 2 8 10 O -10 O 107 -10 -8 4 20 2/ 8 10 -10 8 -6 4 2 0 12 6 8 10 No do do to O O -10 (b) Find the slope of each secant line. (line passing through Q(3, f(x))) (line passing through Q(2.5, f(x))) 60(15 f(x) ) )O (b) Find the slope of each secant line. (line passing through Q(3, f(x))) (line passing through Q(2.5, f(x))) \\:| (line passing through Q(1.5, f(x))) ((3) Use the results of part (b) to estimate the slope of the tangent line to the graph of f at 10(2, 3). E Describe how to improve your approximation of the slope. 0 Choose secant lines that are nearly horizontal. 0 Define the secant lines with points closer to P. 0 Choose secant lines that are nearly vertical. 0 Define the secant lines with points farther away from P