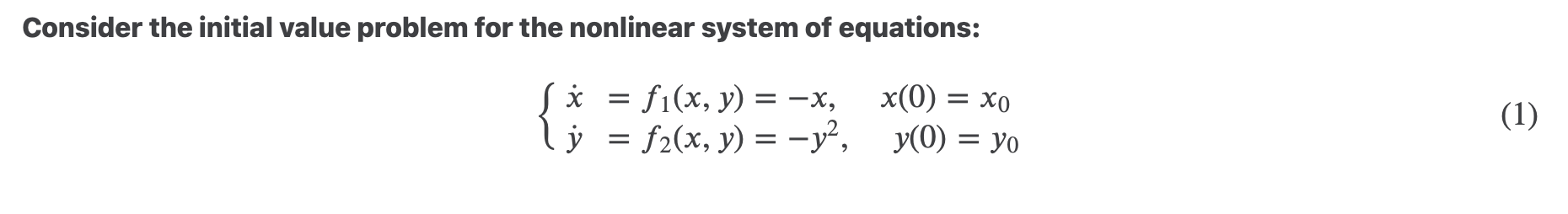
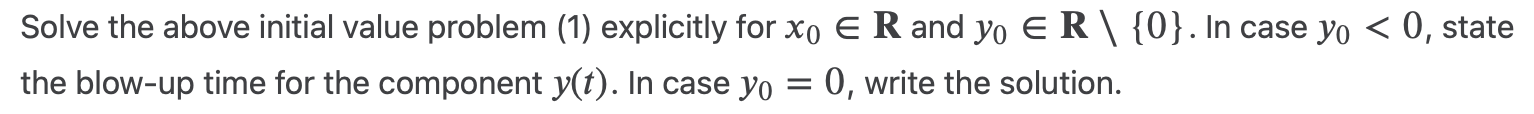
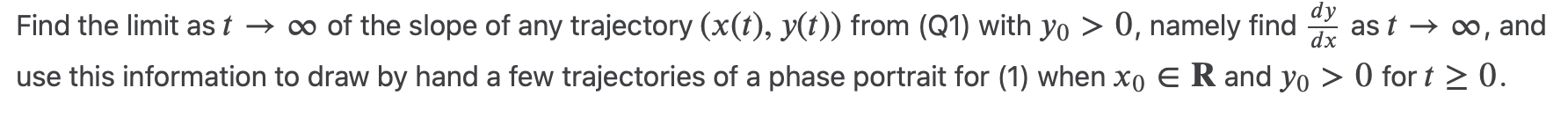
Consider the initial value problem for the nonlinear system of equations: S x = fi(x, y) = -x, x(0) = xo ly = f2(x, y) = -y, (1) y(0) = yoSolve the above initial value problem (1) explicitly for x0 6 R and yo 6 R \\ {0}. In case yo 00 all solutions you found in (Q1) with yo > 0 must approach a fixed point. Find the limit ast > 00 of the slope of any trajectory (x(t), y(t)) from (Q1) with yo > 0, namely find % ast > co, and use this information to draw by hand a few trajectories of a phase portrait for (1) when x0 E R and yo > 0 fort 2 0. Write the first order Taylor polynomial of the functions f1 and f2 around the fixed point (0, 0). Namely write fi (x, y) = %(0, 0)x + 2};(0, 0)y + 0(x2, yz). The linearized system around (0, 0) is: {5c 3'1 Find the fixed point of this linearized system (2), write the solution to (2) with initial data (x0, yo) 6 R2 and draw by hand %(0, 0)x + %(0, my (2) %(0, 0)x + iw, my the phase portrait for (2)