Consider the interval scheduling problem we discussed in class: given a set S = {1, 2, , n} of activities, each activity i has a starting time si and finish time fi. Decide whether each of the following two greedy strategies will return an optimal solution which is a compatible set of maximum size. If the answer is yes, give a proof; if the answer is no, give a counterexample.

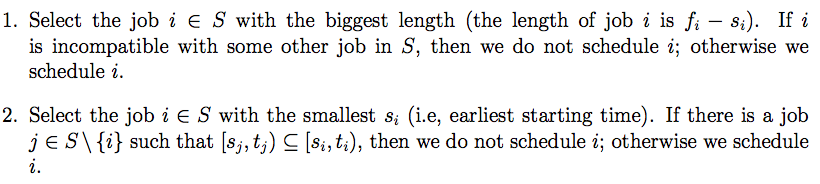
1. Select the job i E S with the biggest length (the length of job i is fi si). If i is incompatible with some other job in S, then we do not schedule i; otherwise we schedule i. 2. Select the job i E S with the smallest si i.e, earliest starting time). If there is a job j E SV such that si,ti) C [si,ti), then we do not schedule i; otherwise we schedule 1. Select the job i E S with the biggest length (the length of job i is fi si). If i is incompatible with some other job in S, then we do not schedule i; otherwise we schedule i. 2. Select the job i E S with the smallest si i.e, earliest starting time). If there is a job j E SV such that si,ti) C [si,ti), then we do not schedule i; otherwise we schedule