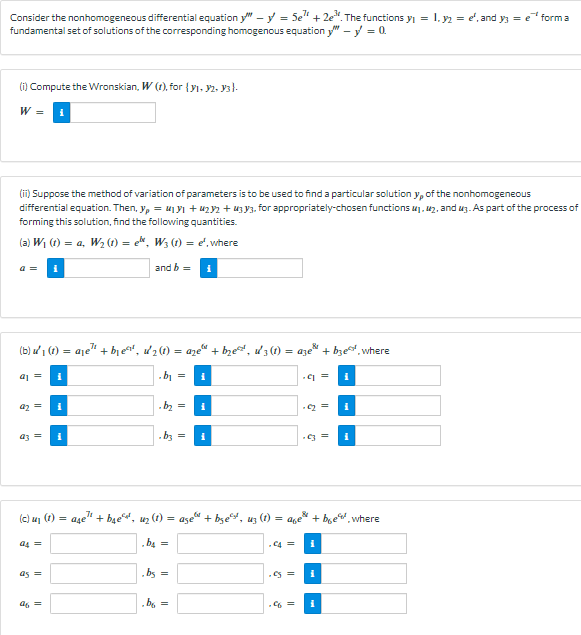
Consider the nonhomogeneous differential equation y" - y = 5e" + 2e". The functions y = 1.yz = e', and ) = e" forma fundamental set of solutions of the corresponding homogenous equation y" - y' = 0. (i) Compute the Wronskian, W (), for (71. )2. x3). W 1 (ii) Suppose the method of variation of parameters is to be used to find a particular solution y, of the nonhomogeneous differential equation. Then, y, = wj)1 + up)2 + ujy/3. for appropriately-chosen functions wj. #2, and uj. As part of the process of forming this solution, find the following quantities. (a) Wi (1) = a, W2 (1) = eh, W} (1) = e. where 1 and b = (bw' (1) = me" + ber, w/2(1) = age" + byed, w/j (1) = ajew + bye. where b1 = i G = 1 1 by = i 1 1 b3 = i 1 (cluj (1) = age" + bye's, my (1) = age"+ bye's, uj (1) = age + byeww. where by = C4 = 1 bs = 4 = i by =