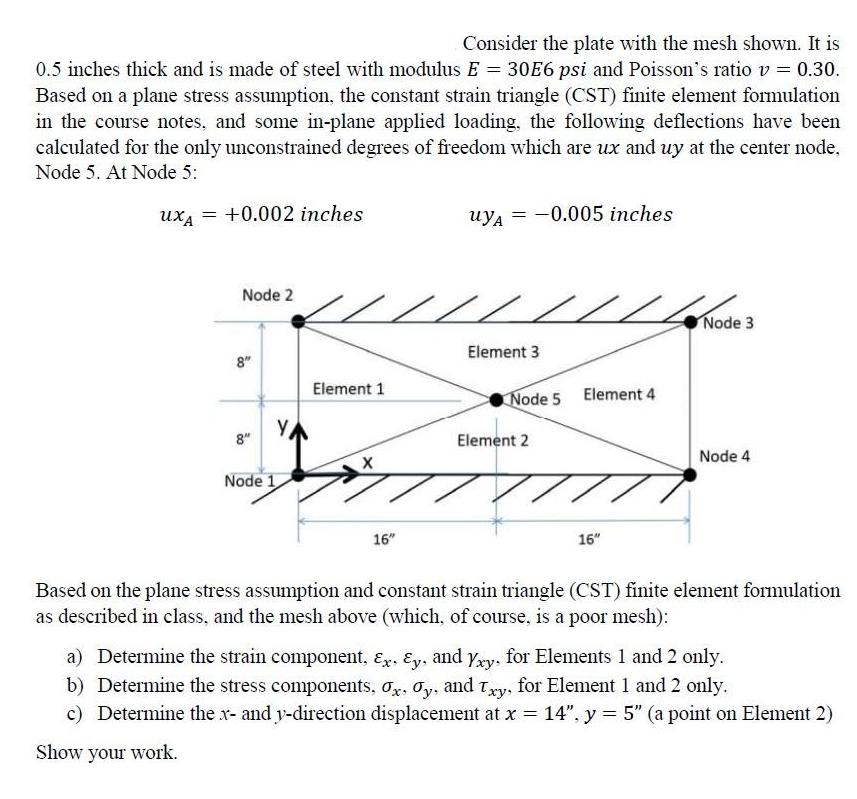
Consider the plate with the mesh shown. It is 0.5 inches thick and is made of steel with modulus E = 30E6 psi and Poisson's ratio v = 0.30. Based on a plane stress assumption, the constant strain triangle (CST) finite element formulation in the course notes, and some in-plane applied loading, the following deflections have been calculated for the only unconstrained degrees of freedom which are ux and uy at the center node. Node 5. At Node 5: uxA= +0.002 inches Node 2 8" 8" Node 1 Y //////Node Node 3 Element 3 Element 1 X uyA= -0.005 inches 16" Node 5 Element 4 Element 2 77 16" Node 4 Based on the plane stress assumption and constant strain triangle (CST) finite element formulation as described in class, and the mesh above (which, of course, is a poor mesh): a) Determine the strain component, Ex. Ey, and Yxy. for Elements 1 and 2 only. b) Determine the stress components, x, y, and Txy, for Element 1 and 2 only. c) Determine the x- and y-direction displacement at x = 14". y = 5" (a point on Element 2) Show your work. Consider the plate with the mesh shown. It is 0.5 inches thick and is made of steel with modulus E = 30E6 psi and Poisson's ratio v = 0.30. Based on a plane stress assumption, the constant strain triangle (CST) finite element formulation in the course notes, and some in-plane applied loading, the following deflections have been calculated for the only unconstrained degrees of freedom which are ux and uy at the center node. Node 5. At Node 5: uxA= +0.002 inches Node 2 8" 8" Node 1 Y //////Node Node 3 Element 3 Element 1 X uyA= -0.005 inches 16" Node 5 Element 4 Element 2 77 16" Node 4 Based on the plane stress assumption and constant strain triangle (CST) finite element formulation as described in class, and the mesh above (which, of course, is a poor mesh): a) Determine the strain component, Ex. Ey, and Yay. for Elements 1 and 2 only. b) Determine the stress components, x, y, and Txy, for Element 1 and 2 only. c) Determine the x- and y-direction displacement at x = 14". y = 5" (a point on Element 2) Show your work.