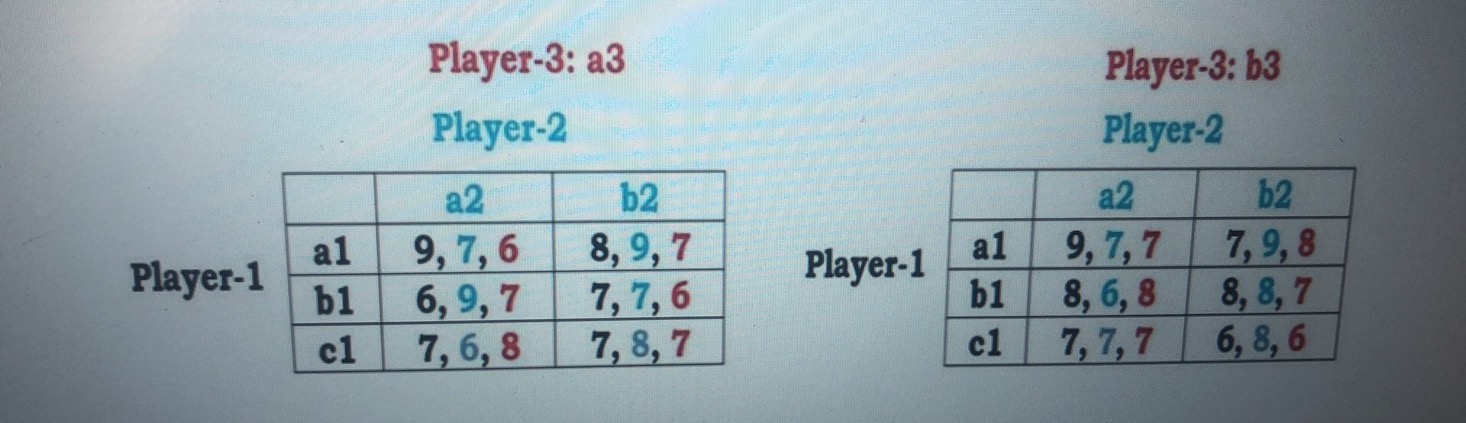
Question: Consider the three-player game shown below. Player 1 selects a row, either a1, b1 or c1. Player 2 selects a column, either a2 or b2.

Consider the three-player game shown below. Player 1 selects a row, either a1, b1 or c1. Player 2 selects a column, either a2 or b2. Player 3 selects a matrix, either a3 or b3. The first number in a cell is player 1's payoff, the second number is player 2's payoff, and the last number is player 3's payoff. Derive the strategies that survive the iterative deletion of strictly dominated strategies.

After IDSDS, does this game have Nash Equilibrium?

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Economics Questions!

solve this question properly. 5(A) Consider the three-player game shown below. Player 1 selects a row, either al, bl or cl. Player 2 selects a column, either a2 or b2. Player 3 selects a matrix,...

a . Consider the three - player game below. Player 1 selects a row, either al , b 1 , or c 1 . Player 2 selects a column, either a 2 , b 2 , or c 2 . Player 3 selects a matrix, either a 3 or b 3 or c...

BA 1605: Midterm Recap (Due: Feb. 27, 2015) Name _____________________________ 50 Student ID _____________________________ Section 01B 10:00~11:20 am Section 02B 01:00~02:20 pm [Questions 4 ~ 7] The...

Create a program to play three mens morris. The program should use a two dimensional vector, to display a 3x3 grid of zeros. a b c 1 : 0 0 0 2 : 0 0 0 3 : 0 0 0 In the main function: Print the board...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

it's a multiple choice with the explanation answer like A or B or C or D it's a multiple choice you can answer more than one choice . three choice or four or two or whateve it's not supposed to be...

In Python: A program to implement the tic-tac-toe (Links to an external site.) game. The user is prompted with three options. A player need to be able to change the characters used for the game in...

Chapter 10 Chapter Exercise Assignment 1. Suppose that the editors of Time and Newsweek are trying to decide upon their cover story for the week. There were two major news developments: The leaking...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

IfyouhaveplayedaSimulationcalledProBankerIneedhelpansweringthesequestionsassoonaspossible from the pro bankerassignment attachment..please use spreadsheet and players manual for reference. Need...

A firm produces a product with labor and capital. Its production function is described by Q = min(L, K). Let w and r be the prices of labor and capital, respectively. a) Find the equation for the...

1. What is the expected 1-year bond yield, 1 year from now? 2. What is the expected 1-year bond yield, 5 years from now? 3. What is the expected 3-year bond yield, 5 years from now? years to maturity...

wildhorse co . Receives 2 9 2 , 8 0 0 when it issues a 2 9 2 , 8 0 0 , 6 % mortgage note payable to finance the construction of a building at devember 3 1 , 2 0 2 5 . The terms provide for annual...

WHAT IS the cash flow statement BBINFIT ,AND HOW WE CAN ANALAYSES

=+ At what rate does capital per person grow?

=+ Compare the marginal product at the Golden Rule steady state to the marginal product in the initial steady state. Explain.

=+ 3. Prove each of the following statements about the steady state of the Solow model with population growth and technological progress.