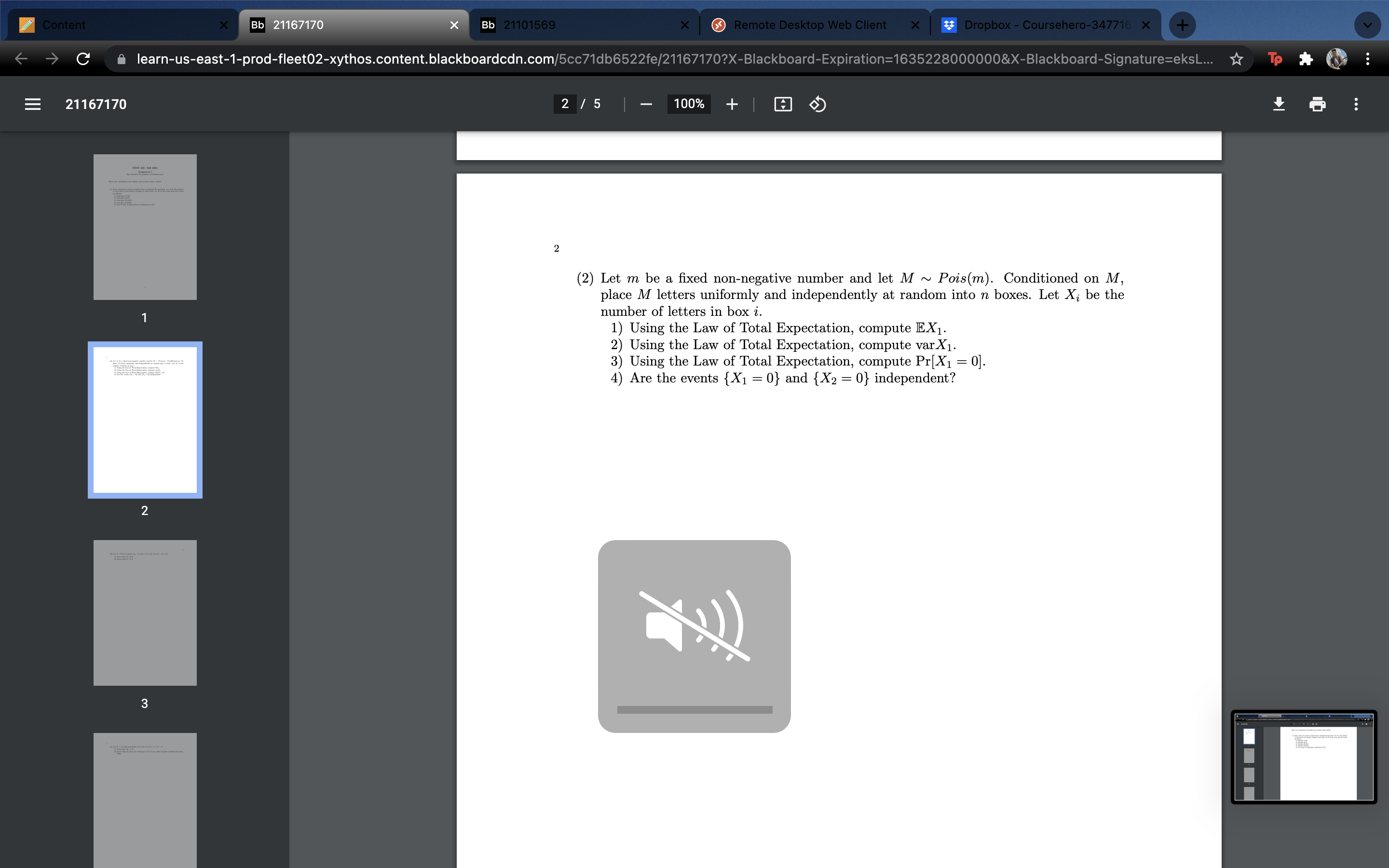
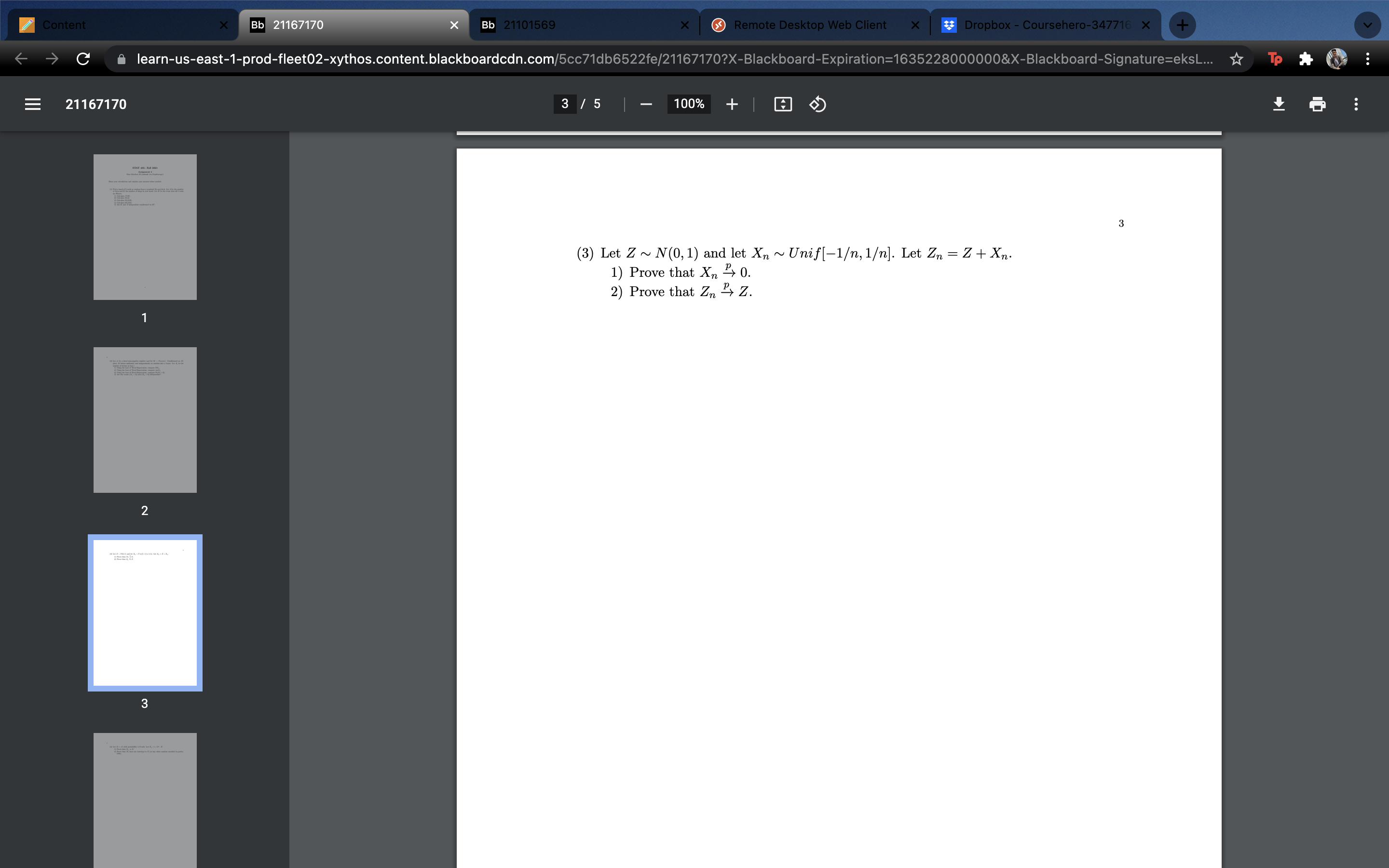
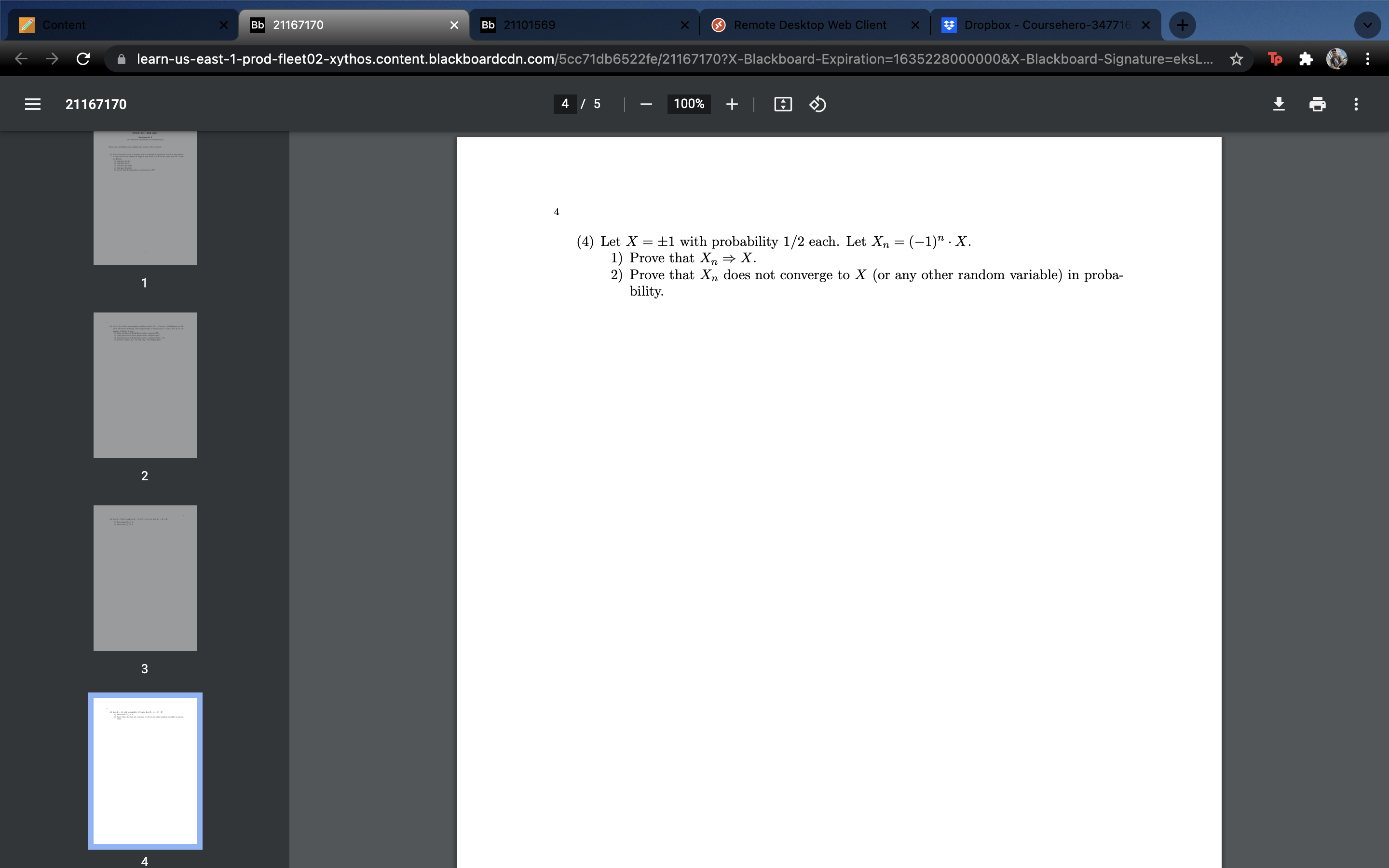
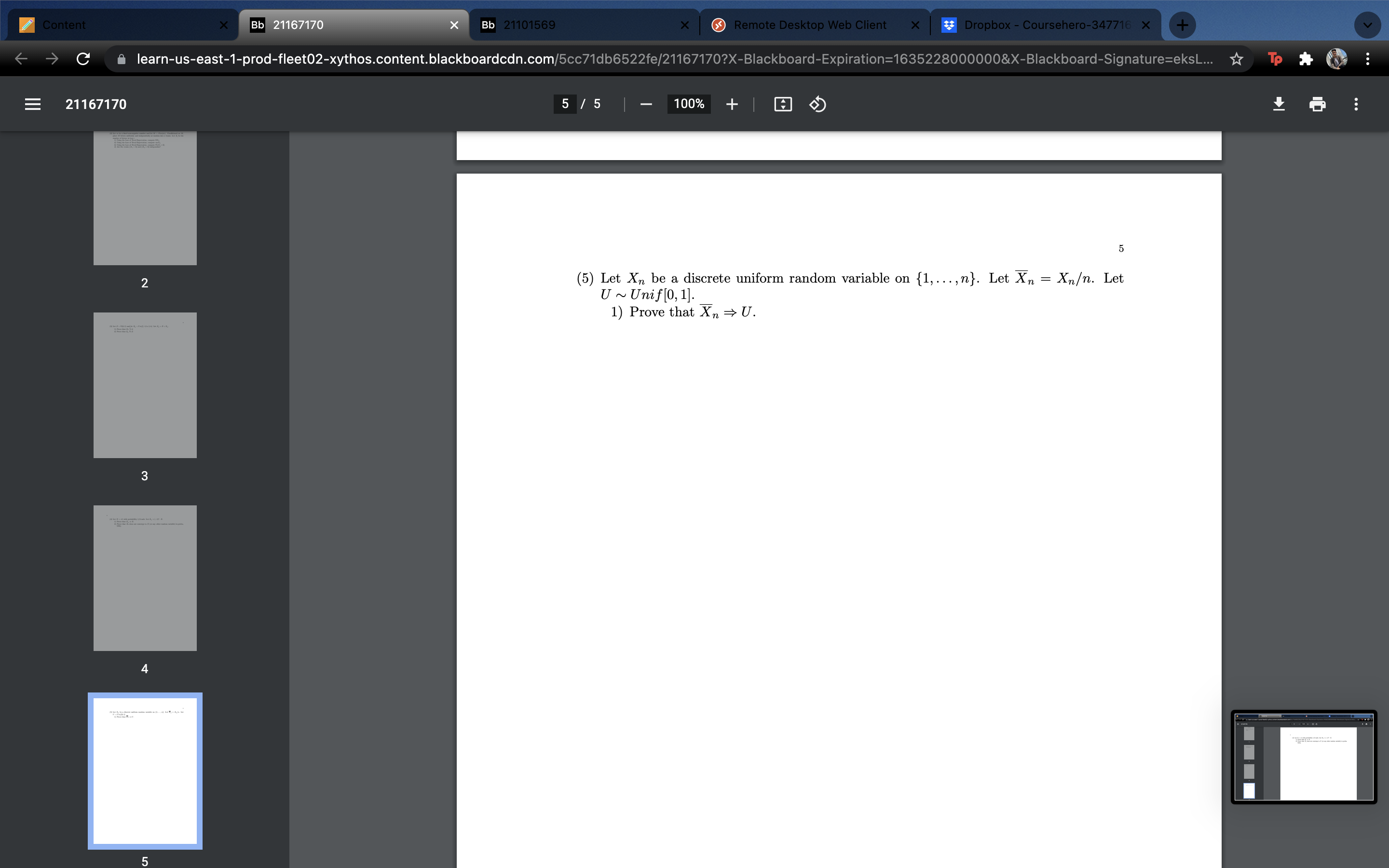
Content Bb 21167170 Bb 21101569 Remote Desktop Web Client X * Dropbox - Coursehero-347716 x C learn-us-east-1-prod-fleet02-xythos.content.blackboardcdn.com/5cc71db6522fe/21167170?X-Blackboard-Expiration=1635228000000&X-Blackboard-Signature=eksL... To 21167170 2 / 5 100% + 2 (2) Let m be a fixed non-negative number and let M ~ Pois(m). Conditioned on M, place M letters uniformly and independently at random into n boxes. Let X; be the number of letters in box i. 1) Using the Law of Total Expectation, compute EX1. 2) Using the Law of Total Expectation, compute var X1. 3) Using the Law of Total Expectation, compute Pr[X1 = 0]. 4) Are the events { X1 = 0} and {X2 = 0} independent? 2 3Content Bb 21167170 Bb 21101569 Remote Desktop Web Client X Dropbox - Coursehero-347716 X C learn-us-east-1-prod-fleet02-xythos.content.blackboardcdn.com/5cc71db6522fe/21167170?X-Blackboard-Expiration=1635228000000&X-Blackboard-Signature=eksL... To 21167170 3 / 5 | 100% + co (3) Let Z ~ N(0, 1) and let Xn ~ Unif[-1, 1]. Let Zn = Z + Xn. 1) Prove that Xn - 0. 2) Prove that Zn "> Z. 1 2 3Content Bb 21167170 Bb 21101569 Remote Desktop Web Client X Dropbox - Coursehero-347716 X C learn-us-east-1-prod-fleet02-xythos.content.blackboardcdn.com/5cc71db6522fe/21167170?X-Blackboard-Expiration=1635228000000&X-Blackboard-Signature=eksL... To 21167170 4 / 5 100% + 4 (4) Let X = +1 with probability 1/2 each. Let Xn = (-1)" . X. 1) Prove that Xn = X 2) Prove that Xn does not converge to X (or any other random variable) in proba- bility . 2 3Content Bb 21167170 Bb 21101569 Remote Desktop Web Client X * Dropbox - Coursehero-347716 x C learn-us-east-1-prod-fleet02-xythos.content.blackboardcdn.com/5cc71db6522fe/21167170?X-Blackboard-Expiration=1635228000000&X-Blackboard-Signature=eksL... To 21167170 5 / 5 100% + 5 2 (5) Let Xn be a discrete uniform random variable on {1, ..., n}. Let Xn = Xn. Let U ~ Unif[0, 1]. 1) Prove that Xn = U. 3