convert this lienar program to paython code plzz

this is the question

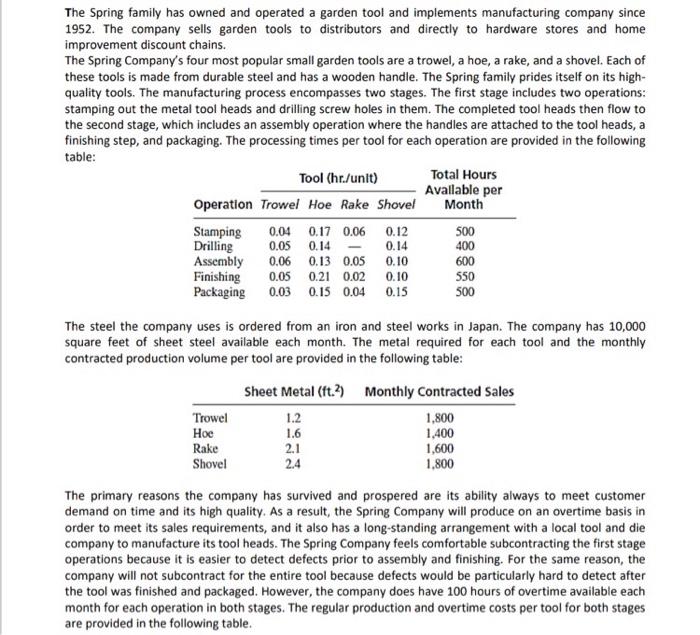
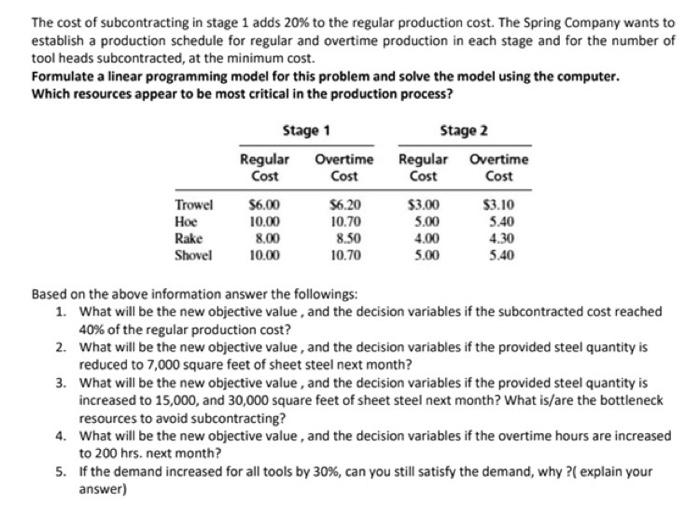
Model Formulation: Let i = 1 (trowel), 2 (hoe), 3 (rake), 4 (shovel) Ri = regular production of product i in stage 1 Si = subcontracted production of product i in stage 1 xi = overtime production of product i in stage 1 Ai = regular production of product i in stage 2 yi = overtime production of product i in stage 2 minimize Z = $6R1 + 10R2 + 8R3 + 10R4 + 7.251 + 1252 + 9.653 + 1254 + 6.2x1 + 10.7x2 + 8.5x3 + 10.7x4 + 3A1 + 5A2 + 4A3 + 5A4 + 3.161 +5.4y2 + 4.3y3 +5.4y4 subject to .04R1 +.17R2 +.06R3 +.12R4 s 500 hrs. .04x1 + 17x2 +.06x3 + 12x4 s 100 hrs. 05R1 +.14R2 + .14R4 s 400 hrs. 05x1 +.14x2 +.14x4 s 100 hrs. 1.2R1 + 1.6R2 + 2.1R3 + 2.4R4 + 1.2x1 + 1.6x2 +2.1x3 + 2.4x4 s 10,000 ft2 .06A1 + .13A2+.05A3 +.10A4 s 600 hrs. 06y1 +.13y2 +.05y3 + .10y4 s 100 hrs. 0541 + 21A2+.02A3 +.10A4 s 550 hrs. 05y1 + 21y2 + .02y3 + 10y4 s 100 hrs. 03A1+.15A2 +.04A3 +.15A4 s 500 hrs. .03y1 +.15y2 +.04y3 + .15y4 s 100 hrs. R1 + S1 + x1 = A1 + y1 R2 + S2 + x2 = A2 + y2 R3+ S3 + x3 = A3+ y3 R4 +S4 + x4 = A4 + y4 y1 + A1 = 1,800 y2 + A2 = 1,400 y3 + A3 = 1,600 y4 + A4 = 1,800 Ri, Si, xi, Ai, yi 2 0 Solution: R1 = 1,691.954 s1 = s2 = s3 = 0 R2 = 1,319.54 s2 = 866.6667 R3 = 1,600 y1 = 0 ZE $85,472.60 R4 = 933.33 y2 = 315.1514 A1 = 1,800 y3 = 0 A2 = 1,084.849 y4 = 388.1822 A3 = 1,600 x1 = 108.0457 A4 = 1,461.818 y2 = 80.4599 x3 = x4 = 0 Let xij be the number of tool i produced at standard costs during stage j. yij be the number of tool i produced at overtime costs at stage j, and zi be the number of tool i produced by the subcontractor. minij cijxij+i/Edijyij+i1.2ciizi subject to: ElisxilsLs iEliDxilsLD iliAxi2sLA iliFxi2sLF EliPxi2sLP igliSyil+iSliDyil 5100 liAyi2+iliFyi2+iliPyi2s100 Emixi1+iE miyils10000 xil+yil+ziznivi xi2+yi2znivi xij.yij,zizo Explanation: For this question, you need to determine the production schedule for both regular and overtime production as well as how much to subcontract out to sell items at minimal cost. To solve this problem, we need to set up a linear programming problem with multiple variables and constraints. Our objective is to minimize the total cost. Let xij be the number of tool i produced at standard costs during stage j. yij be the number of tool i produced at overtime costs at stage j, and zi be the number of tool i produced by the subcontractor. We will define our parameters below: Let cij represent the regular cost to produce tooli in stage j and dij represents the overtime cost to produce tooli in stage j. So, for example, cT1=6 and dT1=6.20 while CT2=3 and dT2=3.10. Similarly, let lik be the labor hours associated with performing action k to produce tool i. Let Lk be the total hours of available labor for action k across the month. So, to stamp a trowel we have ITS =0.04, while the total stamping time available across the month is given by Ls =500. Let mi be the amount of metal needed to produce the tool and ni be the amount of items that must be produced. Then the objective function is: mini,jEcijxij+i,jEdijyij+i81.2cizi Our first set of constraints concerns the labor hours. We factor in the labor to create each tool and the total available regular time hours: iElisxi1sLs iEliDxi1sLD iliAxi2SLA EliFxi2sLF iliPxi2sLP Our second constraints deal with the 100 hours of overtime labor. izliSyi1+iliDyi1 s100 iSliAyi2+iElifyi2+iSlipyi2s100 Our next constraint concerns the amount of metal the company needs to create the tools cannot exceed the the total metal available. imixi1+i{miyi1s10000 Our next constraints state that we must produce enough of each tool in both stage 1 and stage 2 to meet demand. xi 1+yi1+ziznivi xi2+yi2znivi Finally, we need to ensure that all variables are nonnegative. xij.yij,zizo The Spring family has owned and operated a garden tool and implements manufacturing company since 1952. The company sells garden tools to distributors and directly to hardware stores and home improvement discount chains. The Spring Company's four most popular small garden tools are a trowel, a hoe, a rake, and a shovel. Each of these tools is made from durable steel and has a wooden handle. The Spring family prides itself on its high- quality tools. The manufacturing process encompasses two stages. The first stage includes two operations: stamping out the metal tool heads and drilling screw holes in them. The completed tool heads then flow to the second stage, which includes an assembly operation where the handles are attached to the tool heads, a finishing step, and packaging. The processing times per tool for each operation are provided in the following table: Tool (hr./unit) Total Hours Available per Operation Trowel Hoe Rake Shovel Month Stamping 0.04 0.17 0.06 0.12 500 Drilling 0.05 0.14 0.14 400 Assembly 0.06 0.13 0.05 0.10 600 Finishing 0.05 0.21 0.02 0.10 550 Packaging 0.03 0.15 0.04 0.15 500 Hoe 1.6 2.1 The steel the company uses is ordered from an iron and steel works in Japan. The company has 10,000 square feet of sheet steel available each month. The metal required for each tool and the monthly contracted production volume per tool are provided in the following table: Sheet Metal (ft.2) Monthly Contracted Sales Trowel 1.2 1,800 1,400 Rake 1,600 Shovel 24 1.800 The primary reasons the company has survived and prospered are its ability always to meet customer demand on time and its high quality. As a result, the Spring Company will produce on an overtime basis in order to meet its sales requirements, and it also has a long-standing arrangement with a local tool and die company to manufacture its tool heads. The Spring Company feels comfortable subcontracting the first stage operations because it is easier to detect defects prior to assembly and finishing. For the same reason, the company will not subcontract for the entire tool because defects would be particularly hard to detect after the tool was finished and packaged. However, the company does have 100 hours of overtime available each month for each operation in both stages. The regular production and overtime costs per tool for both stages are provided in the following table. The cost of subcontracting in stage 1 adds 20% to the regular production cost. The Spring Company wants to establish a production schedule for regular and overtime production in each stage and for the number of tool heads subcontracted, at the minimum cost. Formulate a linear programming model for this problem and solve the model using the computer. Which resources appear to be most critical in the production process? Stage 1 Regular Overtime Cost Cost $6,00 $6.20 10.00 10.70 8.00 8.50 10.00 10.70 Stage 2 Regular Overtime Cost Cost $3.00 $3.10 5.00 5.40 4.00 4.30 5.00 5.40 Trowel Hoe Rake Shovel Based on the above information answer the followings: 1. What will be the new objective value, and the decision variables if the subcontracted cost reached 40% of the regular production cost? 2. What will be the new objective value, and the decision variables if the provided steel quantity is reduced to 7,000 square feet of sheet steel next month? 3. What will be the new objective value, and the decision variables if the provided steel quantity is increased to 15,000, and 30,000 square feet of sheet steel next month? What is/are the bottleneck resources to avoid subcontracting? 4. What will be the new objective value, and the decision variables if the overtime hours are increased to 200 hrs. next month? 5. If the demand increased for all tools by 30%, can you still satisfy the demand, why ? explain your answer)