could someone help me with the coding on MATLAB for problem a,b,and c for this problem. Please be specific with each problem. Thank you

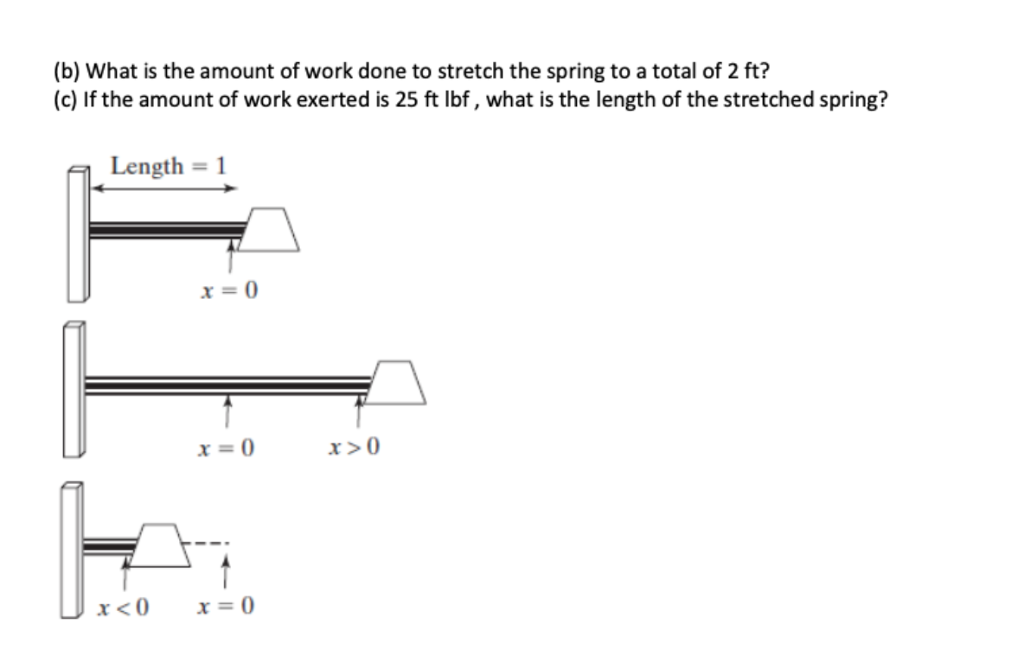
Spring Problem Consider a spring with the left end held fixed and the right end free to move along the x-axis. We assume that the right end of the spring is at the origin x = 0 when the spring is at rest, when the spring is stretched, the right end of the spring is at some new value of x greater than zero. When the spring is compressed, the right end of the spring is at some value less than zero. Suppose that the spring has a natural length of 1 ft and that a force of 10 lb is required to compress it to a length of 0.5 ft. Then, it can be shown that the work, in ft bf performed to stretch the spring from its natural length to a total of n ft is equal to the integral of 20x over the interval from 0 to n -1. (a) Use MATLAB to determine a symbolic expression that represents the amount of work necessary to stretch the spring to a total length of n ft. (Work is the integral of force times the differential of position) Spring Problem Consider a spring with the left end held fixed and the right end free to move along the x-axis. We assume that the right end of the spring is at the origin x = 0 when the spring is at rest, when the spring is stretched, the right end of the spring is at some new value of x greater than zero. When the spring is compressed, the right end of the spring is at some value less than zero. Suppose that the spring has a natural length of 1 ft and that a force of 10 lb is required to compress it to a length of 0.5 ft. Then, it can be shown that the work, in ft bf performed to stretch the spring from its natural length to a total of n ft is equal to the integral of 20x over the interval from 0 to n -1. (a) Use MATLAB to determine a symbolic expression that represents the amount of work necessary to stretch the spring to a total length of n ft. (Work is the integral of force times the differential of position)