Could you explain how to find a complex-valued harmonic function's second derivative by using taylor table? Here's the taylor table for 1st derivative (F')

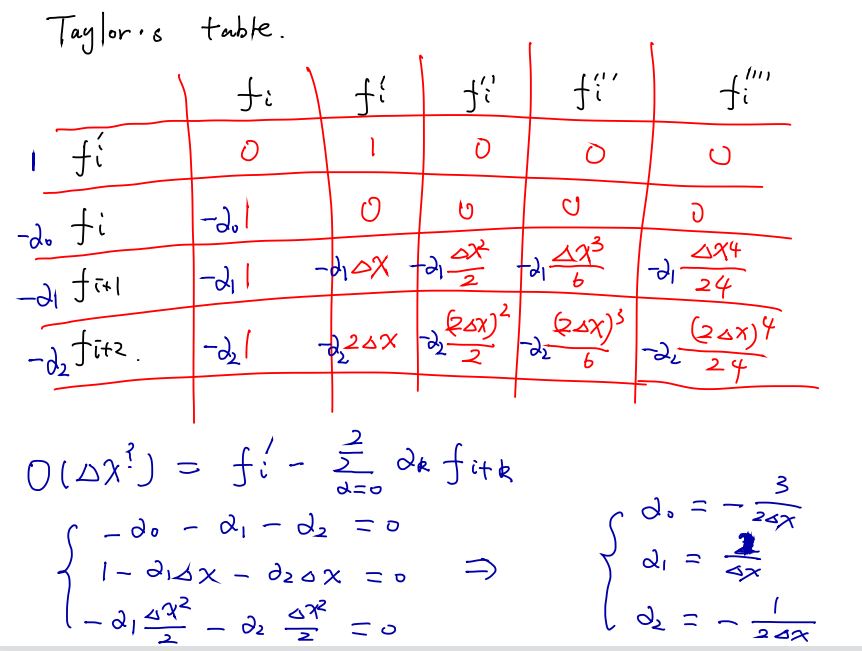
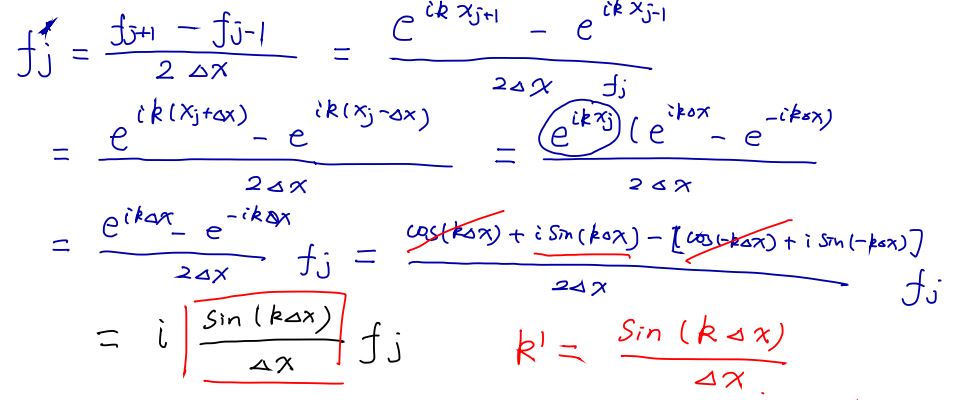
Taylor's table . Fi fi 0 - O -do fi O 474 -21 1 2 24 ( 247 )3 - d, Fitz -22 / -2, 24X 2 2 ( 24X ) 4 2 - 25 6 24 O ( DX. ) = fi - 5 2k fitk d= o 3 - do - 21 - 02 = 0 do = - 25X 1 - 214x - 020X = 0 Q1 = - 2, 472 - 22 2 24XCR X j-1 SSH - JJ-1 e CR Xj +1 e 2 AX 24X ik(X; - ox ) ik xi ckox -iesx) e le e = e e 26X 24X - iRex costRox) + i Sin ( Rox) - [cost-kan) + i sTh (-kox)) 24X 24 X Sin ( k4x R'= Sin ( 4x) 4X 4x0 O O -do fi -201 474 -21 1 di 24 - do Jitz - 2, 1 2, 24X (4X)S ( 2 4 X ) 4 2 6 - 25 24 t != [ de titk + 0 (ox! ) 0 1x') ) = fi - 5 2x fitk. do = 472 - do - 21 - 2 2 = 0 a = - 2 - 21 - 220x = 0 1 - 21 2 - 2, (20x)2 2 = 0 leading term in the truncated error - 2 1 6 - 2, ( 20 X) 6 fi = fi -2 fin+ fitz - exti 472 + Ist 0 ( 4x) fi + fil - 2 fi + fi + . . 4x2 12 0 ( 4x 2)