Question: Could you explain how to find the Poisson Process and the discrete time Markov chain such that we can write the representation Y(t) = X

Could you explain how to find the Poisson Process and the discrete time Markov chain such that we can write the representation Y(t) = X_N(t)?

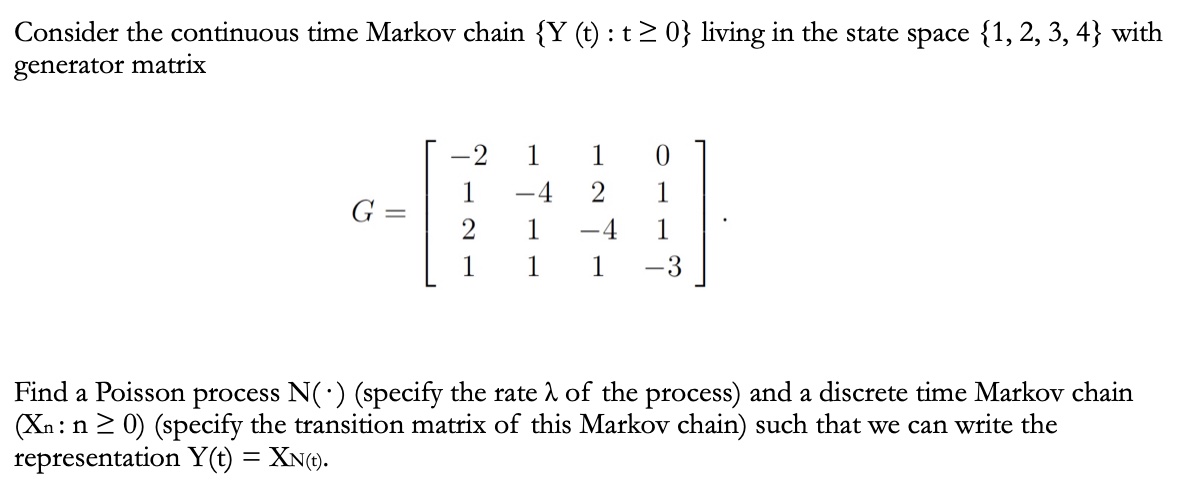
Consider the continuous time Markov chain {Y (t) : t Z 0} living in the state space {1, 2, 3, 4} with generator matrix Find a Poisson process N( ') (specify the rate 7L of the process) and a discrete time Markov chain (X11: n 2 0) (specify the transition matrix of this Markov chain) such that we can write the representation Y(t) = XN(:)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Question 1 ( 50 points) A physical-fitness center has found that, of those members who perform highimpact exercising (1), will either repeat high-impact exercising, or do medium-impact exercising...

Consider the finite queue variation of the M/G/1 model, where K is the maximum number of customers allowed in the system. For n = 1, 2, . . . , let the random variable Xn be the number of customers...

Consider the finite queue variation of the M/G/1 model, where K is the maximum number of customers allowed in the system. For n 1, 2, . . . , let the random variable Xn be the number of customers in...

r each of the following write T (True) or F (False) (no explanation : (a) All nite state space irreducible continuoustime Markov chains have a unique iimiting probability distribution. (b) The...

For each of the following write T (True) or F (False) : (a) All finite state space irreducible continuous-time Markov chains have a unique limiting probability distribution. (b) The counting process...

Consider a discrete time Markov chain with finite or countable state space S and transition matrix II(x, y), x, y E S, so that II(x, y) > 0 is the probability for the Markov chain to jump from z to y...

An economy can be in any of 5 states at any given time, numbered from 1 to 5 , corresponding to worst ( 1 ) to best ( 5 ) . The economy tends to stay in state 3 ( neutral ) , but it can fluctuate...

Hi, please can you answer this Stochastic Processes question for me, thank you. 4. (a) Boy Tom is always in one of three states: eat, play and sleep. He eats on average for 20 minutes at a time;...

6.1. Let Y,,, n = 0, 1, . . . , be a discrete time Markov chain with transition probabilities P = lPA, and let {N(t); t ? 0) be an independent Poisson process of rate A. Argue that the compound...

Number 11.14. Please help me li.14. A small mass m attached to the midpoint of a spring is held between the end points of a track along the X'-axis (Fig. P11.14). The track is fixed on a table that...

Provide a short synthesis of the ester-acid below, starting from maleic acid; see Section 10.1 for a structure of maleic acid. (An ideal synthesis would avoid creating a mixture.)

Question 2 8 2 pts All of these are factors encouraging product adaptation except: Local competition. Economies of scale Differing use conditions. Differing consumer behavior patterns.

What is the difference between pure and mixed IP models? Which do you think is most common, and why?

National Bank loaned the Lyon Company $10 million, at an interest rate of 8%. The note was signed January 1, 2008, and was due December 31, 2022. Annual interest was last paid on December 31, 2016....

Puritan Motors has a capital structure consisting almost entirely of equity. a. If the beta of Puritan stock equals 1.6, the risk-free rate equals 6%, and the expected return on the market portfolio...

Refer to Cornerstone Exercise 7.10. (Round percentages to four significant digits and cost allocations to the nearest dollar.) Required: 1. Calculate the total revenue, total costs, and total gross...

A company manufactures three products, L-Ten, Triol, and Pioze, from a joint process. Each production run costs $12,900. None of the products can be sold at split-off, but must be processed further....

A pizza delivery service wants to track their delivery times in minutes). They took eight samples (one on each of eight days) of four deliveries each and recorded the delivery times in the table...

2. How can the expectations we have of a person contribute to the image we have of him / her? Give some examples from your own everyday life.

9. Discuss the statement: If the actors mainly act on the basis of a view of human-ity as driven by self-interest, and incorporate this idea into their models, they may end up with their premises...

5. What does it mean when we say the evaluation comes before the presenta-tion?.