could you help with these

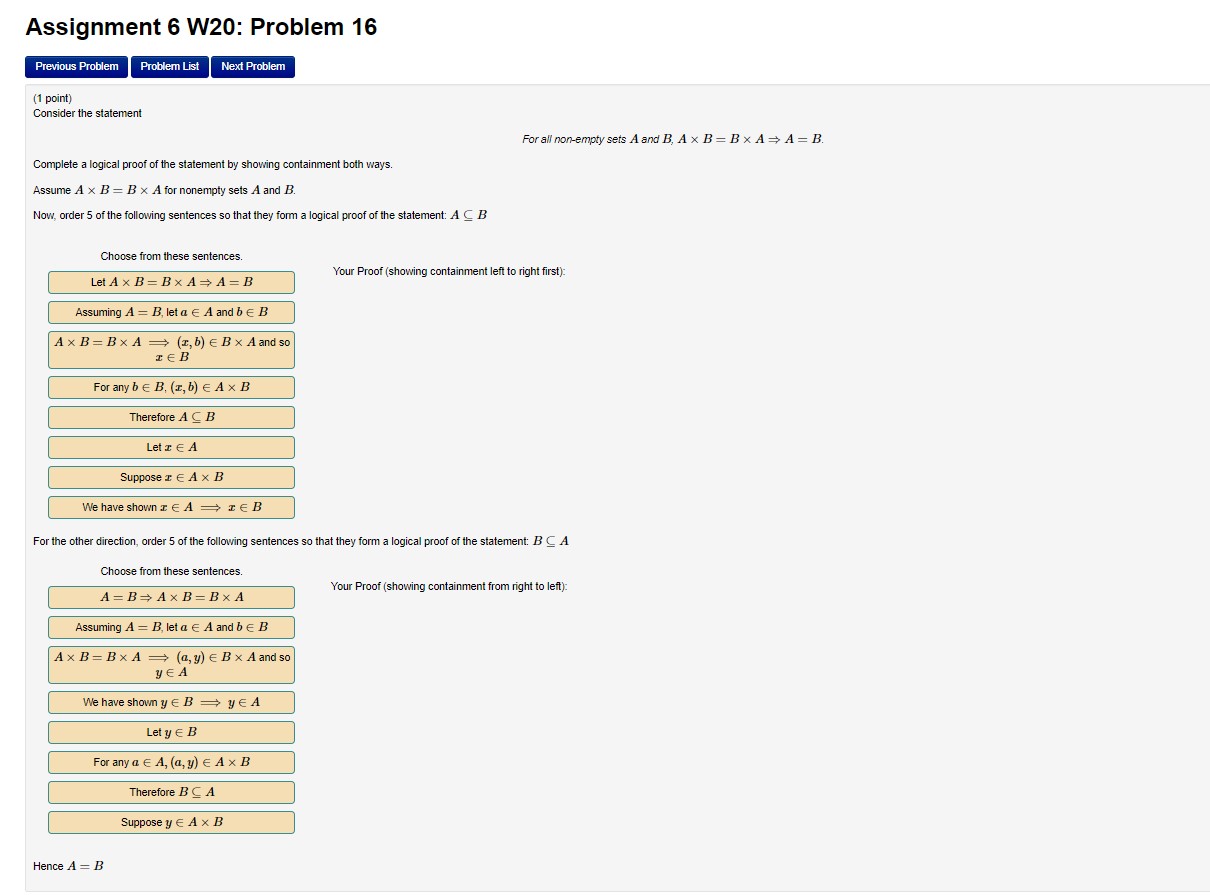
Assignment 6 W20: Problem 16 Previous Problem Problem List Next Problem (1 point) Consider the statement For all non-empty sets A and B, A x B = B x A = A= B Complete a logical proof of the statement by showing containment both ways. Assume A x B = B x A for nonempty sets A and B. Now, order 5 of the following sentences so that they form a logical proof of the statement: A C B Choose from these sentences. Let A x B = B x A = A=B Your Proof (showing containment left to right first): Assuming A = B, let a E A and be B A x B = B x A = (1, b) E B x A and so IEB For any b E B, (1, b) E A x B Therefore A C B Let I E A Suppose T E A x B We have shown : ( A => I E B For the other direction, order 5 of the following sentences so that they form a logical proof of the statement: B C A Choose from these sentences. A=B= AXB=B XA Your Proof (showing containment from right to left): Assuming A = B, let a E A and b E B A x B = B x A => (a, y) E B x A and so YEA We have shown y E B - ye A Let y E B For any a E A, (a, y) E A x B Therefore B C A Suppose y E A x B Hence A = BAssignment 6 W20: Problem 17 {1 point) Order 8 of the following sentences so that they form a logical proof of the statement: [Start with \"Suppose B and D are sets" as your rst statement] 30(3) u 13(1)) g 19(3 u D) Choose from these sentences: Your Proof: Eis a subset ofBU 1). 17(3) and 29(1)} are nonempty since all power ] sets contain at least the empty set. Without loss of generality, assume E is an element of 13(3). E is an element of ?(B) or E is an element of 'P(D). E is an element of P{B U D) Let E be an element of 13(3) U 13(1)). ] E is an element of B U D ] Suppose B and D are sets. E is a subset of B