Hi, can someone help me with these questions?

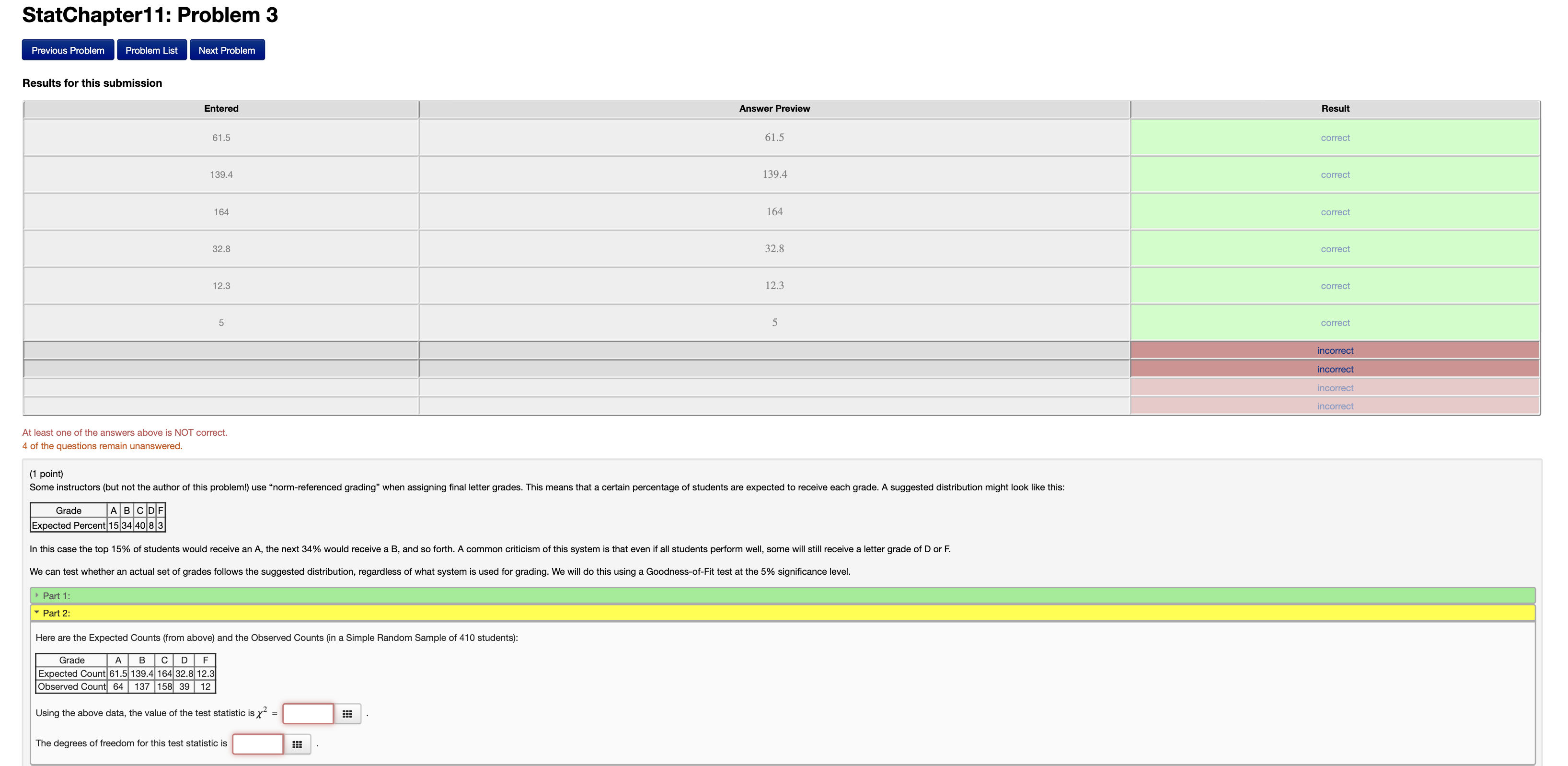
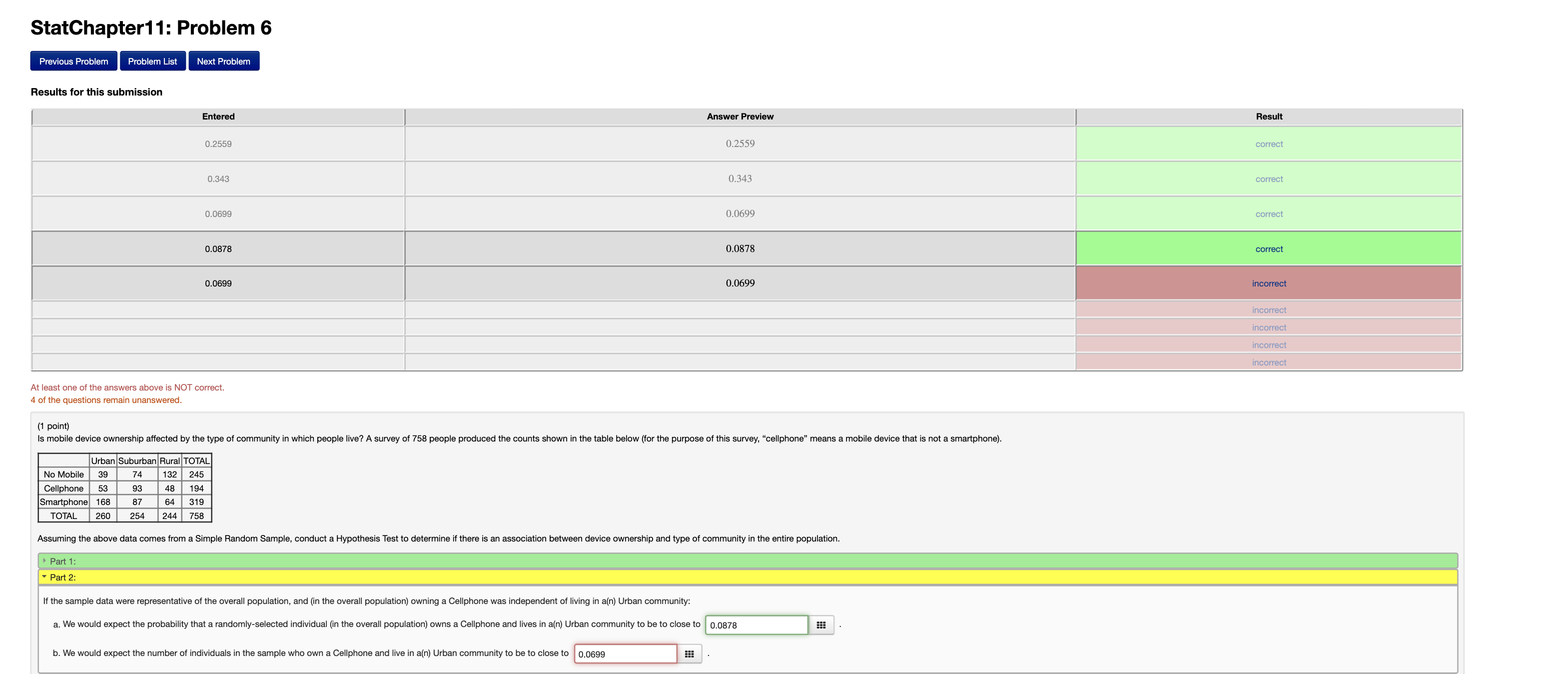
StatChapter11: Problem 3 Previous Problem Problem List Next Problem Results for this submission Entered Answer Preview Result 61.5 61.5 correct 139.4 139.4 correct 164 164 correct 32.8 32.8 correct 12.3 12.3 correct 5 5 correct incorrect incorrect incorrect incorrect At least one of the answers above is NOT correct. 4 of the questions remain unanswered. (1 point) Some instructors (but not the author of this problem!) use "norm-referenced grading" when assigning final letter grades. This means that a certain percentage of students are expected to receive each grade. A suggested distribution might look like this: Grade ABC DF Expected Percent 15 34 40 8 3 In this case the top 15% of students would receive an A, the next 34% would receive a B, and so forth. A common criticism of this system is that even if all students perform well, some will still receive a letter grade of D or F. We can test whether an actual set of grades follows the suggested distribution, regardless of what system is used for grading. We will do this using a Goodness-of-Fit test at the 5% significance level. Part 1: - Part 2: Here are the Expected Counts (from above) and the Observed Counts (in a Simple Random Sample of 410 students): Grade A B CDF Expected Count 61.5 139.4 164 32.8 12.3 Observed Count 64 137 158 39 12 Using the above data, the value of the test statistic is x = The degrees of freedom for this test statistic isStatChapter11: Problem 6 Previous Problem Problem List Next Problem Results for this submission Entered Answer Preview Result 0.2559 0.2559 correct 0.343 0.343 correct 0.0699 0.0699 correct 0.0878 0.0878 correct 0.0699 0.0699 incorrect incorrect incorrect incorrect incorrect At least one of the answers above is NOT correct. 4 of the questions remain unanswered (1 point) Is mobile device ownership affected by the type of community in which people live? A survey of 758 people produced the counts shown in the table below (for the purpose of this survey, "cellphone" means a mobile device that is not a smartphone). Urban Suburban Rural TOTAL No Mobile 39 74 132 245 Cellphone 53 93 48 194 Smartphone 168 87 64 319 TOTAL 260 254 244 758 Assuming the above data comes from a Simple Random Sample, conduct a Hypothesis Test to determine if there is an association between device ownership and type of community in the entire population. Part 1: . Part 2: If the sample data were representative of the overall population, and (in the overall population) owning a Cellphone was independent of living in a(n) Urban community: a. We would expect the probability that a randomly-selected individual (in the overall population) owns a Cellphone and lives in a(n) Urban community to be to close to 0.0878 b. We would expect the number of individuals in the sample who own a Cellphone and live in a(n) Urban community to be to close to 0.0699