Cross$-$correlation $(28$ points$)$

We are building our own Acoustic Positioning System.

NOTE: The signatures vec$($s$)\_(1),$vec$($s$)\_(2)$ in each sub$-$part are different; each prompt is independent from the others.

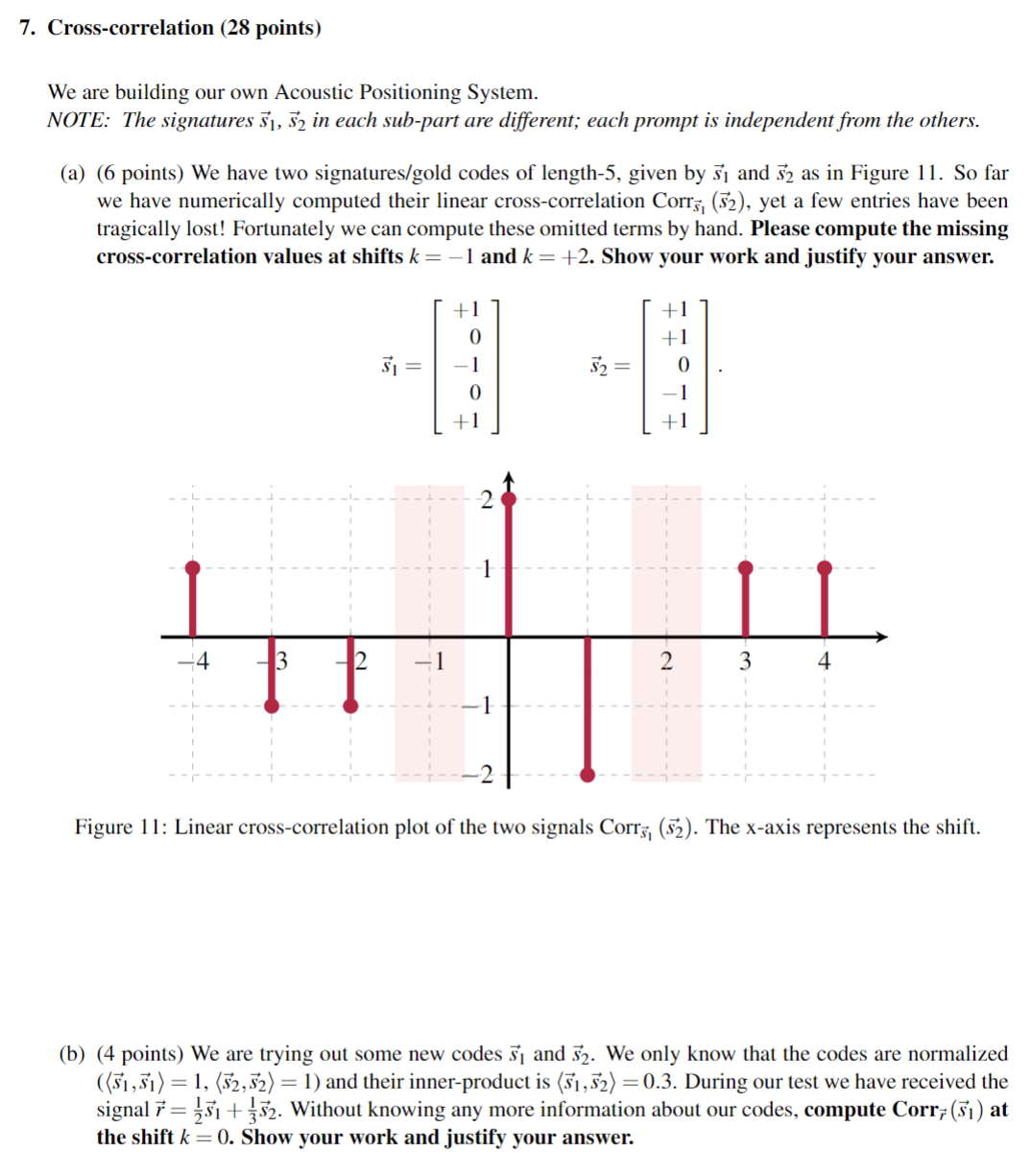
$($a$)(6$ points$)$ We have two signature$($s$)/($g$)$old codes of length$-5,$ given by vec$($s$)\_(1)$ and vec$($s$)\_(2)$ as in Figure $11.$ So far

we have numerically computed their linear cross$-$correlation Corr$\_($vec$($s$)\_(1))($vec$($s$)\_(2)),$ yet a few entries have been

tragically lost! Fortunately we can compute these omitted terms by hand. Please compute the missing

cross$-$correlation values at shifts k$=-1$ and k$=+2.$ Show your work and justify your answer.

vec$($s$)\_(1)=[[+1],[0],[-1],[0],[+1]],$vec$($s$)\_(2)=[[+1],[+1],[0],[-1],[+1]]$

Figure $11$: Linear cross$-$correlation plot of the two signals Corr$\_($vec$($s$)\_(1))($vec$($s$)\_(2)).$ The x $-$axis represents the shift.

$($b$)(4$ points$)$ We are trying out some new codes vec$($s$)\_(1)$ and vec$($s$)\_(2).$ We only know that the codes are normalized

$(($:vec$($s$)\_(1),$vec$($s$)\_(1)$:$)=1,($:vec$($s$)\_(2),$vec$($s$)\_(2)$:$)=1)$ and their inner$-$product is $($:vec$($s$)\_(1),$vec$($s$)\_(2)$:$)=0\mathrm{.}3.$ During our test we have received the

signal vec$($r$)=(1)/(2)$vec$($s$)\_(1)+(1)/(3)$vec$($s$)\_(2).$ Without knowing any more information about our codes, compute Corr$\_($vec$($r$))($vec$($s$)\_(1))$ at

the shift k$=0.$ Show your work and justify your answer.

$($c$)(4$ points$)$ We again have two new signals vec$($s$)\_(1)$ and vec$($s$)\_(2),$ and are now given the plot of Corr$\_($vec$($s$)\_(1))($vec$($s$)\_(2))$ as shown

in Figure $12.$ Our receiver identified a signal vec$($r$)$ which we know to be related to the code vec$($s$)\_(2)$ by some

scaling, shifting, an$($d$)/($o$)$r reflection. However, we only know the linear cross$-$correlation Corr$\_($vec$($s$)\_(1))($vec$($r$))$ as

shown in Figure $13.$ Can you express vec$($r$)$ in terms of vec$($s$)\_(2)?$ Show your work and justify your answer.

Figure $12$: Linear cross$-$correlation plots for Corr$\_($vec$($s$)\_(1))($vec$($s$)\_(2)).$

Figure $13$: Linear cross$-$correlation plots for Corr$\_($vec$($S$)\_(1))($vec$($r$)).$

$($d$)(4$ points$)$ With a little effort we managed to create two good gold codes of length $100,$vec$($s$)\_(1)$ and vec$($s$)\_(2).$ The linear cross$-$correlation of vec$($s$)\_(1)$ and vec$($s$)\_(2)$ is small at all shifts while the autocorrelation of each signal is also small, except at shift k$=0.$ We receive our first signal vec$($r$)$ which we know to be a combination of both codes

vec$($r$)[$n$]=$vec$($s$)\_(1)[$n$-$k$\_(1)]+$vec$($s$)\_(2)[$n$-$k$\_(2)].$

The linear cross$-$correlation Corr$\_($vec$($r$))($vec$($s$)\_(1))$ has been computed and plotted in Figure $14,$ and similarly Corr$\_($vec$($r$))($vec$($s$)\_(2))$ is plotted in Figure $15.$ Determine the shifts for vec$($s$)\_(1)$ and vec$($s$)\_(2)$ in the received signal vec$($r$),$ i$.$e$.$ solve for k$\_(1)$ and k$\_(2)$ in equation $(3).$ Explain your answer.

Note: Don't worry too much about identifying the exact value for k$\_(1)$ and k$\_(2).$ As long as your answer is reasonable, you will receive full credit.

Figure $14$: Linear cross$-$correlation piots ior corr$\_($vec$($r$))($s$\_(1)).$

$($f$)(6$ points$)$ After optimizing two orthogonal codes vec$($s$)\_(1)$ and vec$($s$)\_(2)($:vec$($s$)\_(1),$vec$($s$)\_(2)$:$)=0$ vec$($s$)\_(3)$ and make it orthogonal to vec$($s$)\_(1)$ and vec$($s$)\_(2).$ We can start by writing vec$($s$)\_(3)$ as

vec$($s$)\_(3)=$vec$($a$)+$vec$($b$),$ such that vec$($a$)$ belongs to the span $\{$vec$($s$)\_(1),$vec$($s$)\_(2)\}$ and vec$($b$)$ is orthogonal to span $\{$vec$($s$)\_(1),$vec$($s$)\_(2)\},$ i$.$e$.($:$($vec$($b$)),$vec$($s$)\_(1)$:$)=0$

and $($:$($vec$($b$)),$vec$($s$)\_(2)$:$)=0.$ Use the idea of projections to write both vec$($a$)$ and vec$($b$)$ in terms of vec$($s$)\_(1),$vec$($s$)\_(2),$ and vec$($s$)\_(3),$ and

inner$-$products thereof. $($For full credit your final answer may not contain matrices nor matrix$-$

vector products$).$ Show your work and justify your answer.