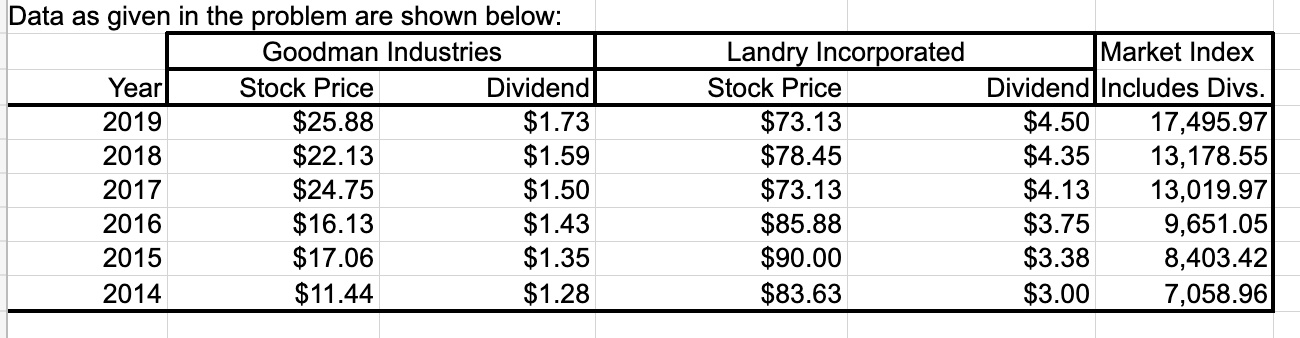
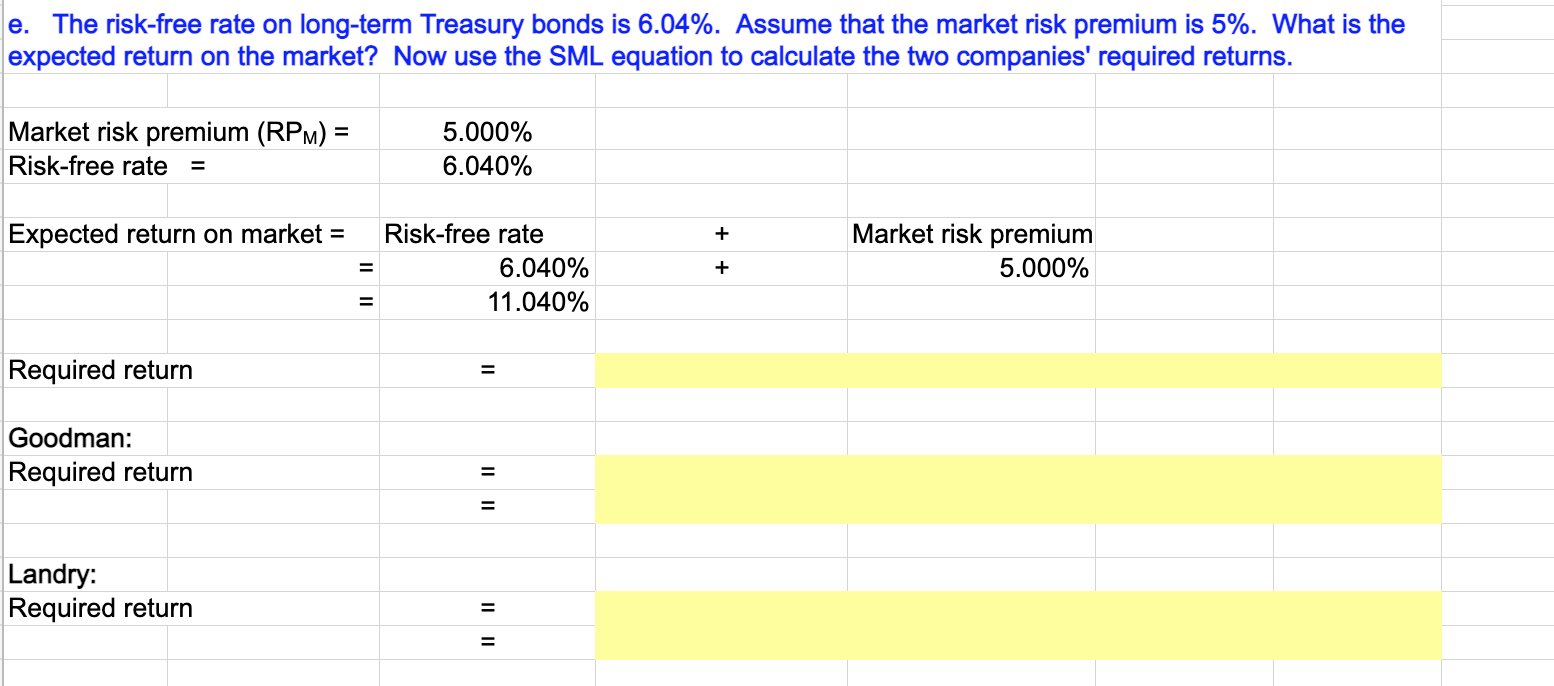
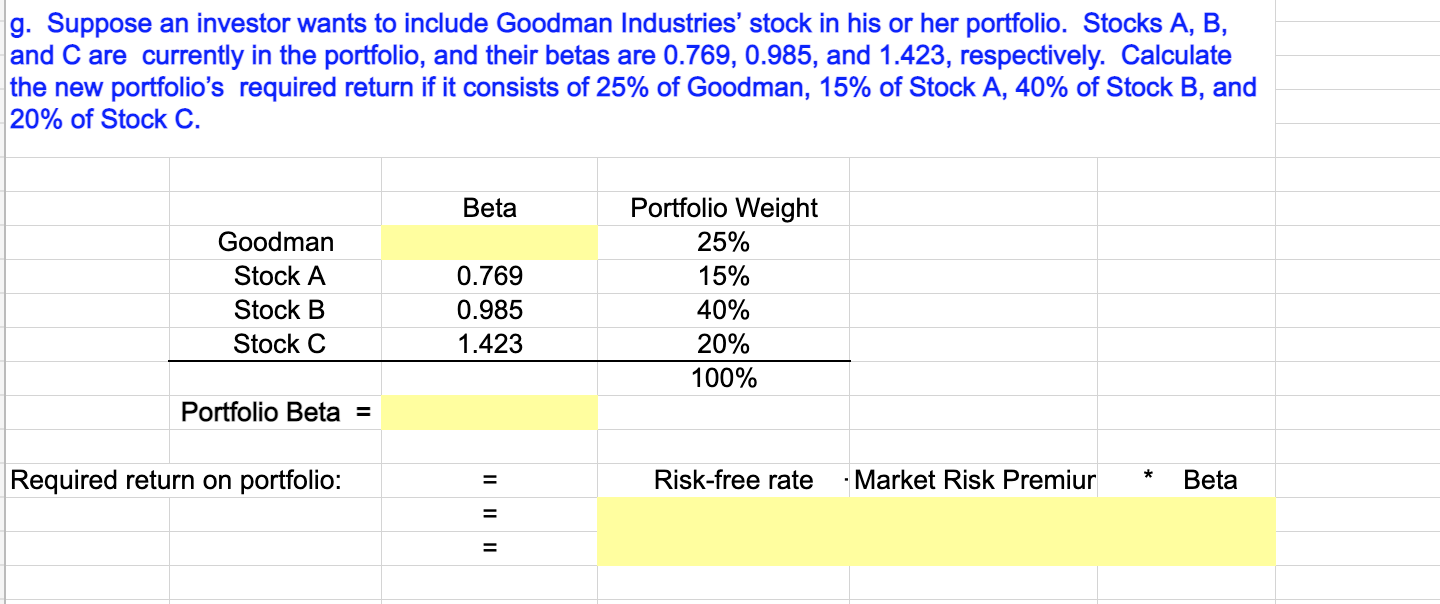
Data as given in the problem are shown below: Goodman Industries Year Stock Price Dividend 2019 $25.88 $1.73 2018 $22.13 $1.59 2017 $24.75 $1.50 2016 $16.13 $1.43 2015 $17.06 $1.35 2014 $11.44 $1.28 Landry Incorporated Stock Price $73.13 $78.45 $73.13 $85.88 $90.00 $83.63 Market Index Dividend Includes Divs. $4.50 17,495.97 $4.35 13,178.55 $4.13 13,019.97 $3.75 9,651.05 $3.38 8,403.42 $3.00 7,058.96 d. Estimate Goodman's and Landry's betas as the slopes of regression lines with stock returns on the vertical axis (y-axis) and market return on the horizontal axis (x-axis). (Hint: use Excel's SLOPE function.) Are these betas consistent with your graph? Goodman's beta = Landry' beta = e. The risk-free rate on long-term Treasury bonds is 6.04%. Assume that the market risk premium is 5%. What is the expected return on the market? Now use the SML equation to calculate the two companies' required returns. Market risk premium (RPM) = Risk-free rate 5.000% 6.040% Expected return on market = + Risk-free rate 6.040% 11.040% Market risk premium 5.000% + Required return = Goodman: Required return = 1 Landry: Required return f. If you formed a portfolio that consisted of 50% Goodman stock and 50% Landry stock, what would be its beta and its required return? The beta of a portfolio is simply a weighted average of the betas of the stocks in the portfolio, so this portfolio's beta would be: Portfolio beta = g. Suppose an investor wants to include Goodman Industries' stock in his or her portfolio. Stocks A, B, and C are currently in the portfolio, and their betas are 0.769, 0.985, and 1.423, respectively. Calculate the new portfolio's required return if it consists of 25% of Goodman, 15% of Stock A, 40% of Stock B, and 20% of Stock C. Beta Goodman Stock A Stock B Stock C 0.769 0.985 1.423 Portfolio Weight 25% 15% 40% 20% 100% Portfolio Beta = Required return on portfolio: Risk-free rate * - Market Risk Premiur Beta = = Data as given in the problem are shown below: Goodman Industries Year Stock Price Dividend 2019 $25.88 $1.73 2018 $22.13 $1.59 2017 $24.75 $1.50 2016 $16.13 $1.43 2015 $17.06 $1.35 2014 $11.44 $1.28 Landry Incorporated Stock Price $73.13 $78.45 $73.13 $85.88 $90.00 $83.63 Market Index Dividend Includes Divs. $4.50 17,495.97 $4.35 13,178.55 $4.13 13,019.97 $3.75 9,651.05 $3.38 8,403.42 $3.00 7,058.96 d. Estimate Goodman's and Landry's betas as the slopes of regression lines with stock returns on the vertical axis (y-axis) and market return on the horizontal axis (x-axis). (Hint: use Excel's SLOPE function.) Are these betas consistent with your graph? Goodman's beta = Landry' beta = e. The risk-free rate on long-term Treasury bonds is 6.04%. Assume that the market risk premium is 5%. What is the expected return on the market? Now use the SML equation to calculate the two companies' required returns. Market risk premium (RPM) = Risk-free rate 5.000% 6.040% Expected return on market = + Risk-free rate 6.040% 11.040% Market risk premium 5.000% + Required return = Goodman: Required return = 1 Landry: Required return f. If you formed a portfolio that consisted of 50% Goodman stock and 50% Landry stock, what would be its beta and its required return? The beta of a portfolio is simply a weighted average of the betas of the stocks in the portfolio, so this portfolio's beta would be: Portfolio beta = g. Suppose an investor wants to include Goodman Industries' stock in his or her portfolio. Stocks A, B, and C are currently in the portfolio, and their betas are 0.769, 0.985, and 1.423, respectively. Calculate the new portfolio's required return if it consists of 25% of Goodman, 15% of Stock A, 40% of Stock B, and 20% of Stock C. Beta Goodman Stock A Stock B Stock C 0.769 0.985 1.423 Portfolio Weight 25% 15% 40% 20% 100% Portfolio Beta = Required return on portfolio: Risk-free rate * - Market Risk Premiur Beta = =