Dear Expert The following below is a MATLAB program that uses the Detrended fluctuation Analysis to find the the slope of the line relating log F(n) to log n determines the scaling exponent (self-similarity parameter), using the following Algorithm and theory shown just here

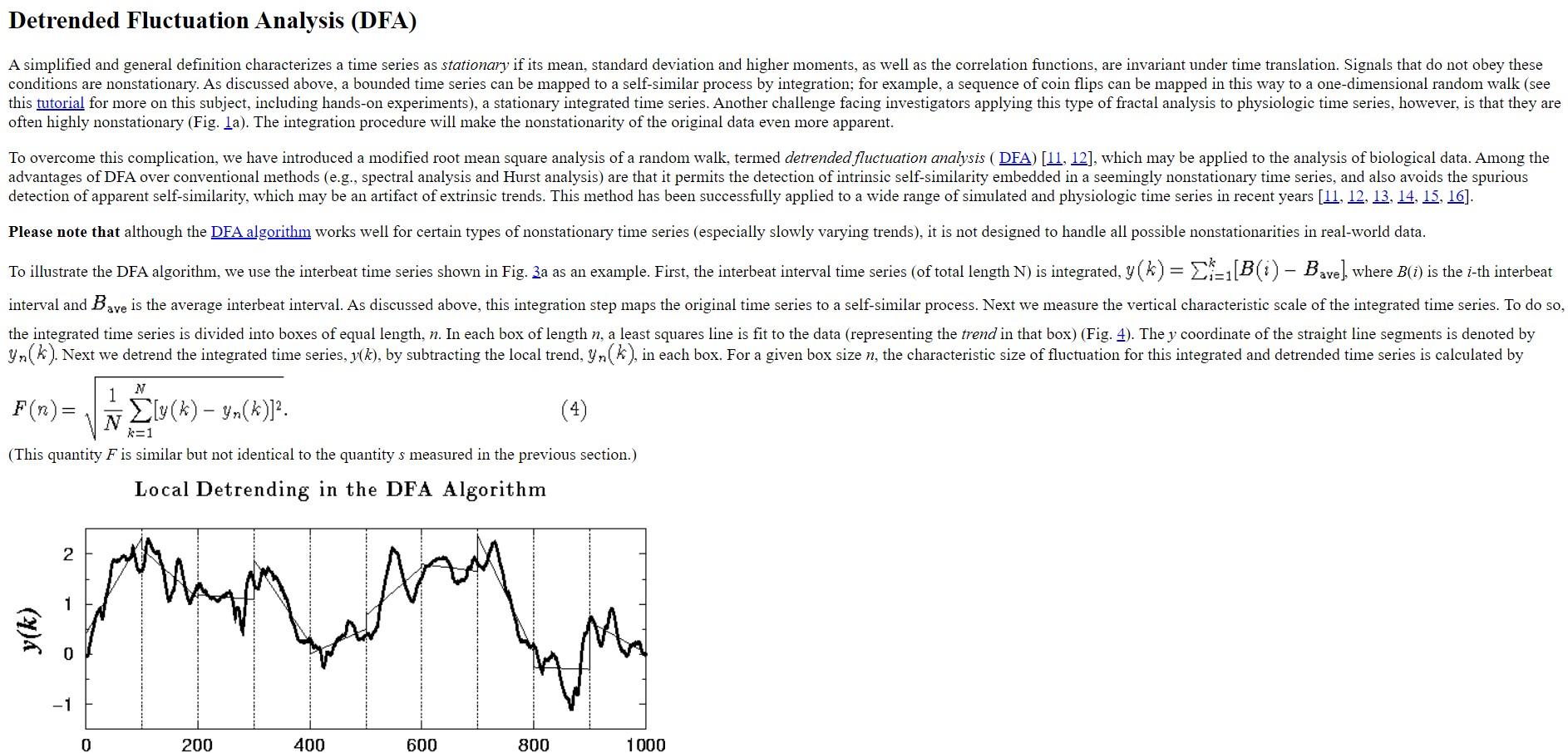
In program below there are errors from line 40 i.e ' fluctuation = zeros(1,k);' in the command prompt it says 'Error using zeros Size inputs must be scalar.in program123 Error (line 40) fluctuation = zeros(1,k); '. Can you help me correct the code and obtain the 'LOCAL DETRENDING GRAPH FOR MY DATA'.

'

%% Import the text from the file "Taking Responsibility for Your Own Actions pdf.docx" filename = "Taking Responsibility for Your Own Actions pdf.docx"; str = extractFileText(filename); % Preprocess the text by removing punctuation and converting all characters to lowercase str1 = erasePunctuation(str); % Split the text into individual words str2=split(str); %Length of word k=length(str2); %Number of words x=[1:k]; % Map each word to its corresponding index of length for i=x:k k(i) = strlength(str2(i)); end

y = k;

%Plot the random walk time series figure(1) plot(x,y) title('Time Series Plot (Number of Letters against Position of Words)') xlabel('Position of words') ylabel('Number of letters') grid on

numpts=20; llimit=2; rlimit=6; lgboxlength=linspace(llimit,rlimit,numpts); boxlength= floor(10.^lgboxlength);

%% Calc Fluctuation for each Boxlength s and calc Fsquared for j= 1:numpts nterms1=boxlength(j); nboxes=floor(kterms1); fluctuation = zeros(1,k); %THERE IS AN ERROR HERE PLEASE CAN YOU HELP ME CORRECT IT %% Calc Trend in Each box of length s and calc Fsquared for i=1:nboxes start =(i-1)*nterms1+1; finish=i*nterms1; x=[start:finish]; a=polyfit(x,y(start:finish),1); trend_segment=a(1)*x+a(2); trend(start:finish)=trend_segment; fluctuation(start:finish)=y(start:finish)-trend_segment; end f(j)=sqrt(mean(fluctuation .^2)); clear trend end %% plotting the log-log Graph Figure(2) plot(log10(boxlength),log10(f),'+k-') title('Detrended Time Series Plot (Number of Letters against Position of Words)') xlabel('Position of words(x)') ylabel('y(k)')

In the end we should obtain the following results .Please check for errors in the code before sending the corrected one .Also can you show me how to :

%% Plot the integrated Time Series

%% CaLCULATE Gradient and its error for whole graph

%% Plotting the best fit line

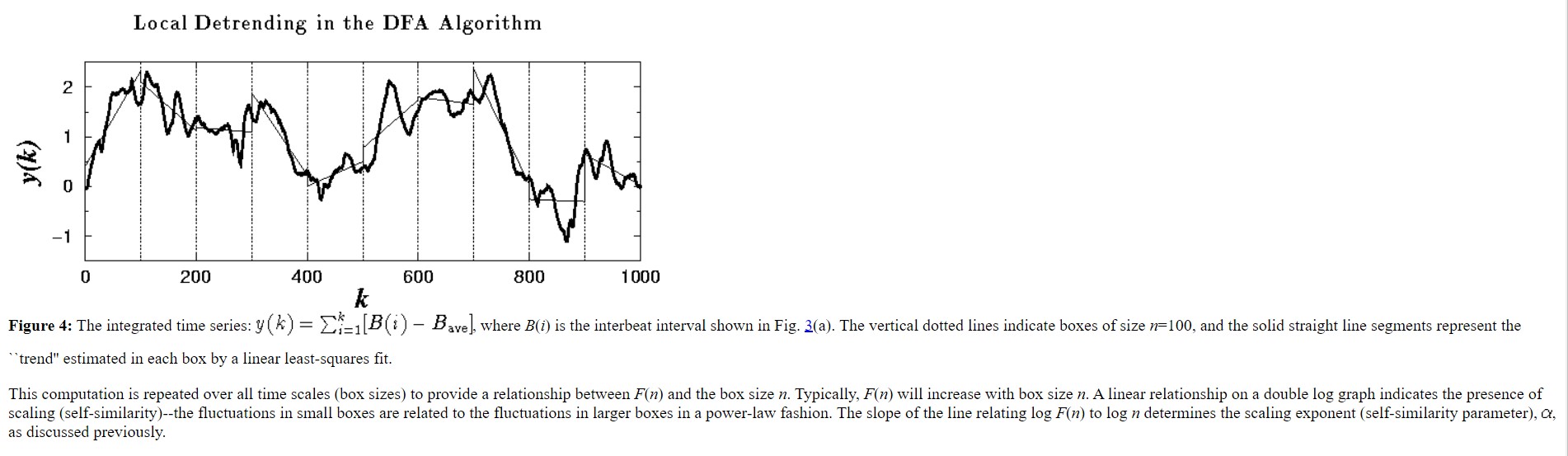
often highly nonstationary (Fig. 1 a). The integration procedure will make the nonstationarity of the original data even more apparent. F(n)=N1k=1N[y(k)yn(k)]2. (This quantity F is similar but not identical to the quantity s measured in the previous section.) Local Detrending in the DFA Algorithm Local Detrending in the DFA Algorithm Figure 4: The integrated time series: y(k)=i=1k[B(i)Bave], where B(i) is the interbeat interval shown in Fig. 3 (a). The vertical dotted lines indicate boxes of size n=100, and the solid straight line segments represent the "trend" estimated in each box by a linear least-squares fit. This computation is repeated over all time scales (box sizes) to provide a relationship between F(n) and the box size n. Typically, F(n) will increase with box size n. A linear relationship on a double log graph indicates the presence of scaling (self-similarity)--the fluctuations in small boxes are related to the fluctuations in larger boxes in a power-law fashion. The slope of the line relating logF(n) to logn determines the scaling exponent (self-similarity parameter), , as discussed previously