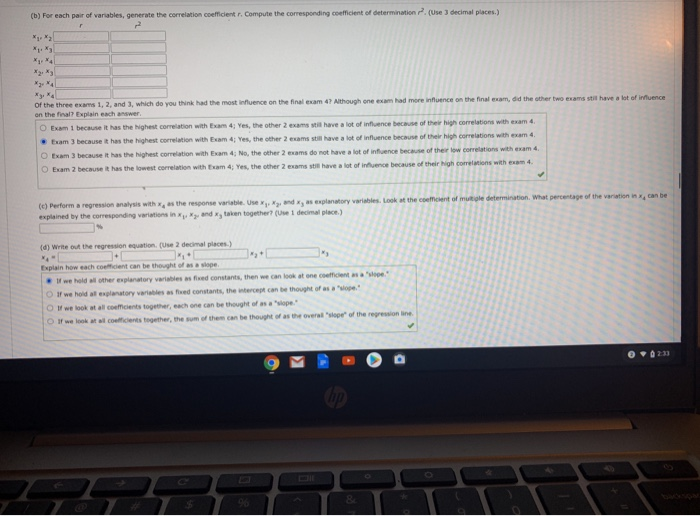
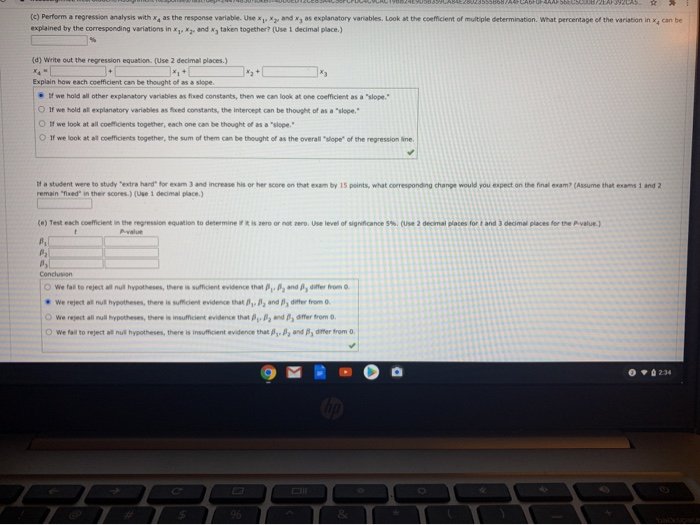
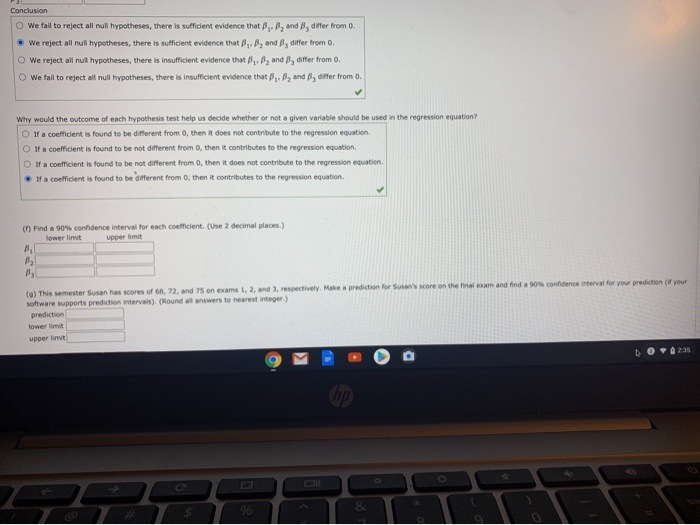
DETAILS MY NOTES A. [0/0.45 Points] BBUNDERSTAT12 0,4004. ASK YOUR TEACHER PRACTICE ANOTHER PREVIOUS ANSWERS Professor Gill has bought General Psychology for many years. During the semester, she gives three multiple-choice exams, each worth 100 points. At the end of the course, Or. Gill gives a comprehensive final worth 200 points. Let ,. My, and x, represent a student's scores on exama 1, 1, and ], respectively. Let s, represent the student's score on the final exam. Last semester Or. Gil had 15 students in her class. The student exam scores are shown below 73 80 75 152 100 73 142 53 45 55 149 47 56 60 115 79 175 164 141 141 184 148 147 177 159 177 175 83 85 175 93 192 There Professor Gul has not changed the course much from last semester to the present semester, the preceding dota should be useful for constructing a regression model that describes this semester as well Ca) Generate summary statistics, including the mean and standard deviation of each variable. Compute the coefficient of variation for each variable. (Uin 2 decimal places. ) CV Relative to its mean, would you say that each exam had about the same spread of wares? Most professors do not wish to give an exam that is extremely easy or extremely hard. Would you say that all of the comma were about the same level of difficulty? (Consider both meara and spread of test scores.) OM N(b) For each pair of variables, generate the correlation coefficient r, Compute the corresponding coefficient of determination . (Use 3 decimal places.) Of the three exams 1, 2, and ], which do you think had the most Influence on the final exam 47 Although one exam had more influence on the final exam, did the other two exams stil have a lot of influence on the final? Explain each grower Q Exam 1 because it has the highest correlation with Exam 4; Yes, the other 2 exaims Mill have a lot of influence because of their high correlations with exam d From 3 because it has the highest correlation with Exam 4; Yes, the other 2 exams still have a lot of influence because of their high correlations with exam 4. O Exam 3 because It has the highest correlation with Exam 4; No, the other 2 exams do not have a lot of influence because ow correlations with exam s. Q. Exam 2 because it has the lowest correlation with Team 4; Yes, the other 2 exams still have a lot of influence because of their high comelations with exum 4. (c) Perform a regression analysis with a, as the response variable. Use a;, My, and s, as explanatory variables. Look at the coefficient of multiple determination. What percentage of the variation in s, can be explained by the corresponding variations in Kj Njy and a, taken together? (Use 1 decimal place.) (dj Write out the regrewion equation, (Use 2 decimal places.) Explain how each confident can be thought of as a slope. If we hold all other explanatory va ables as fixed constant, then we can look at one coefficient as a "slips." If we hold all explanatory variables as fixed constants, the intercept can be thought of as a "slope." If we look at all coufficients together, each one can be thought of as a "slope." if we look at al coollicients together, the sum of them can be thought of as the overall "slope" of the regrenion line. 9 M hp 9%[c) Perform a regression analysis with x, as the response variable. Use *. *, and x, as explanatory variables. Look at the confficient of multiple determination. What percentage of the variation in x, can be explained by the corresponding variations in *,. *; and an taken together? (Use 1 decimal place.) (d) Write out the regression equation. (Use 2 decimal places.) J+L Explain how each coefficient can be thought of as a slope. If we hold all other explanatory variables as fixed constants, then we can look at one coefficient as a "slope." Q If we hold all explanatory variables as fixed constants, the intercept can be thought of as a "slope." If we look at all coefficients together, each one can be thought of as a "slope." O if we look at all coefficients together, the sum of them can be thought of as the overall "slope" of the regression line. if a student were to study "extra hard" for exam 3 and increase his or her score on that exam by 15 points, what corresponding change would you expect on the final exam? (Assume that exam 1 and 2 remain "fixed" in their scores.) (Use 1 decimal place.) (e) Test each confficient in the regression equation to determine If It is zero or not zero. Uve level of significance 514. (Use 2 decimal places for f and 3 decimal places for the Pvalue] Conclusion We fall to reject al null hypotheses, there is sufficient evidence that Aj, fly and f, differ from a. We reject all null hypotheses, there is sufficient evidence that fly, fly and #, differ from 0. Q We reject all rull hypotheses, there is insufficient evidence that /j,fly and fly differ from 0. We fall to reject all null hypotheses, there is insufficient evidence that fly. #, and Ay differ from 0. OM hp C 96Conclusion We fall to reject all null hypotheses, there is sufficient evidence that A, B, and , differ from o " We reject all null hypotheses, there is sufficient evidence that S,. 8, and B, differ from 0. We reject all null hypotheses, there is insufficient evidence that #, , #, and #, differ from 0. ( We fail to reject all null hypotheses, there is insufficient evidence that . By and 6, differ from 0. Why would the outcome of each hypothesis test help us decide whether or not a given variable should be used in the regression equation? O 1f a coefficient is found to be different from 0, then it does not contribute to the regression equation. If a coefficient is found to be not different from 0, then it contributes to the regression equation. O If a coefficient is found to be not different from 0, then it does not contribute to the regression equation. If a coefficient is found to be different from 0; then it contributes to the regression equation. (f) Find a 90% confidence interval for each coefficient. (Use 2 decimal places.) lower limit upper limit (9) This semester Susan has scores of 68, 72, and 75 on exams 1, 2, and 3, respectively. Make a prediction for Susan's score on the final exam and find a 90% confidence interval for your prediction (if your software supports prediction Intervals). (Round ell answers to nearest integer.) prediction lower limit upper limit OM hp C 9%