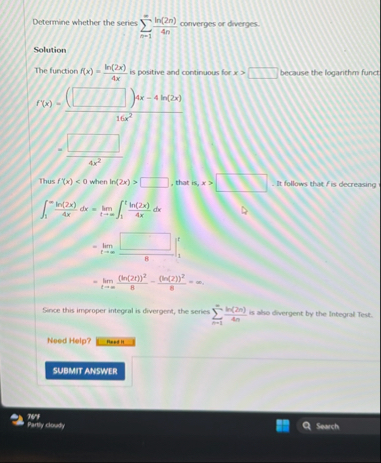
Determine whether the series ${\displaystyle \underset{n=1}{\overset{}{}}}\frac{ln(2n)}{4n}$ converges or diverges.

Solution

The function $f(x)=\frac{ln(2x)}{4x}$ is positive and continuous for $x>$ because the loganthm funct

$f^{\text{'}}(x)=\frac{1}{16x}$

$=\frac{\frac{1}{4x^2}}{16x}$

Thus $f^{\text{'}}(x)<mn>0</mn>$ when $ln(2x)>,$ that is$,x>-$ It follows that fis decreasing

${\displaystyle \underset{1}{\overset{}{}}}\frac{ln(2x)}{4x}dx=\underset{t}{lim}{\displaystyle \underset{1}{\overset{t}{}}}\frac{ln(2x)}{4x}dx$

$=\underset{t}{lim}\frac{?}{8}{|}_1^t|$

$=\underset{t}{lim}\frac{(ln(2t){)}^2}{8}-\frac{(ln(2){)}^2}{8}=$

Sance this improper integral is divergent, the series ${\displaystyle \underset{n=1}{\overset{}{}}}\frac{ln(2n)}{4n}$ is also divergent by the Integral Test. Need Help? $$

$304$

Party downy

Servech