Question: Develop a linear programming model to minimize cost. (Let x ij be the number of square yards of carpet which flows from node i to

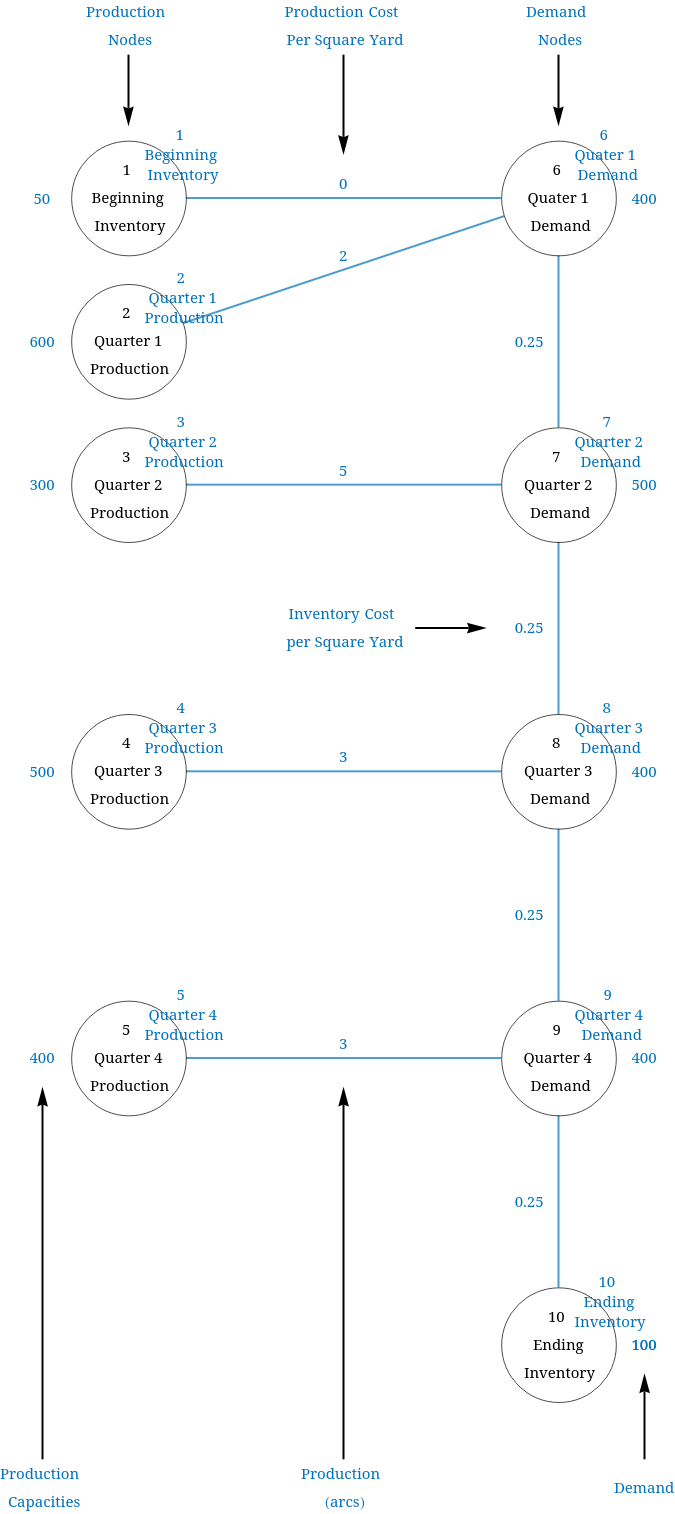
Develop a linear programming model to minimize

Develop a linear programming model to minimize cost. (Let x_ij be the number of square yards of carpet which flows from node i to node j.)

Min 0x16+2x26+5x37+3x48+3x59+0.25x67+0.25x78+0.25x89+0.25x910 (right)

s.t.

Beginning Inventory Flow X16=50 (wrong)

Quarter 1 Production Flow X26600 (wrong)

Quarter 2 Production Flow X37300 (wrong)

Quarter 3 Production Flow X48500 (wrong)

Quarter 4 Production Flow X59400 (wrong)

Quarter 1 Demand Flow X16+X26X67=400 (wrong)

Quarter 2 Demand Flow X37+X67X78=500 (wrong)

Quarter 3 Demand Flow X48+X78X89=400 (wrong)

Quarter 4 Demand Flow X59+X89X910=400 (wrong)

Ending Inventory Flow X910=100 (wrong)

I just need help with the ones I got wrong (in bold). Thank you in advance!!

Production Production Cost Demand Nodes Per Square Yard Nodes 6 Quater 1 6 Demand 0 Beginning 1 Inventory Beginning Inventory 50 400 Quater 1 Demand 2 Quarter 1 2 Production Quarter 1 Production 600 0.25 3 Quarter 2 3 Production 5 300 Quarter 2 Production Quarter 2 7 Demand Quarter 2 500 Demand Inventory Cost per Square Yard 0.25 4 Quarter 3 4 Production Quarter 3 Production 3 500 Quarter 3 8 Demand Quarter 3 400 Demand 0.25 3 Quarter 4 5 Production Quarter 4 Production Quarter 4 9 Demand Quarter 4 400 Demand 400 0.25 10 Ending 10 Inventory Ending Inventory 100 Production Production Demand Capacities (arcs)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

Contois Carpets is a small manufacturer of carpeting for home and office installations. Production capacity, demand, production cost per square yard (in dollars), and inventory holding cost per...

***please help with the incorrect answer**** Contois Carpets is a small manufacturer of carpeting for home and office installations. Production capacity, demand, production cost per square yard (in...

DO NOT COPY PASTE FROM OTHER CHEGG. I ALREADY GOT A COPY PASTE. ITS WRONG. for honest experts, im really sorry for the attitude. Contols Carpets is a small manufacturer of carpeting for home and...

Can yo please show me what exactly goes into each box! Thank you! Contals Carpets is a small manufacturer of carpeting for home and office Installations. Production capacity, demand, production cost...

could someone Give me the correct answers you don't have to show work on how you got the answers just write down the answers Contois Carpets is a small manufacturer of carpeting for home and office...

[ 7 . 3 9 / 1 6 Points ] Develop a linear programming model to minimize cost. ( Let x i j be the number of square yards of carpet which flows from node i to node j . ) Min 0 x 1 6 + 2 x 2 6 + 5 x 3 7...

Develop a linear programming model to minimize cost. ( Let x i j be the number of square yards of carpet which flows from node i to node j . ) Min s . t . Beginning Inventory Flow Quarter 1...

Contois Carpets is a small manufacturer of carpeting for home and office installations. Production capacity, demand, production cost per square yard (in dollars), and inventory holding cost per...

2 (5 Marks) A student borrowed an educational loan of $100,000 at an interest rate of 10% per year and repaired equal payment of S1000 at the end of cach year starting from year 2 to year S The...

X Corp's net accounts receivable were P 250,000 at Dec 31, 2019 and P 300,000 at Dec 31, 2020. Net cash sales for 2020 are P 100,000 and the accounts receivable turnover for 2020 was 5. What were the...

The most well - known retirement plan in U . S . companies today is the variable pay vesting utilization analysis 4 0 1 ( k )

atch the compensation objectives with their meanings. Efficiency Efficiency drop zone empty. Fairness Fairness drop zone empty. Compliance Compliance drop zone empty. Improving performance and...