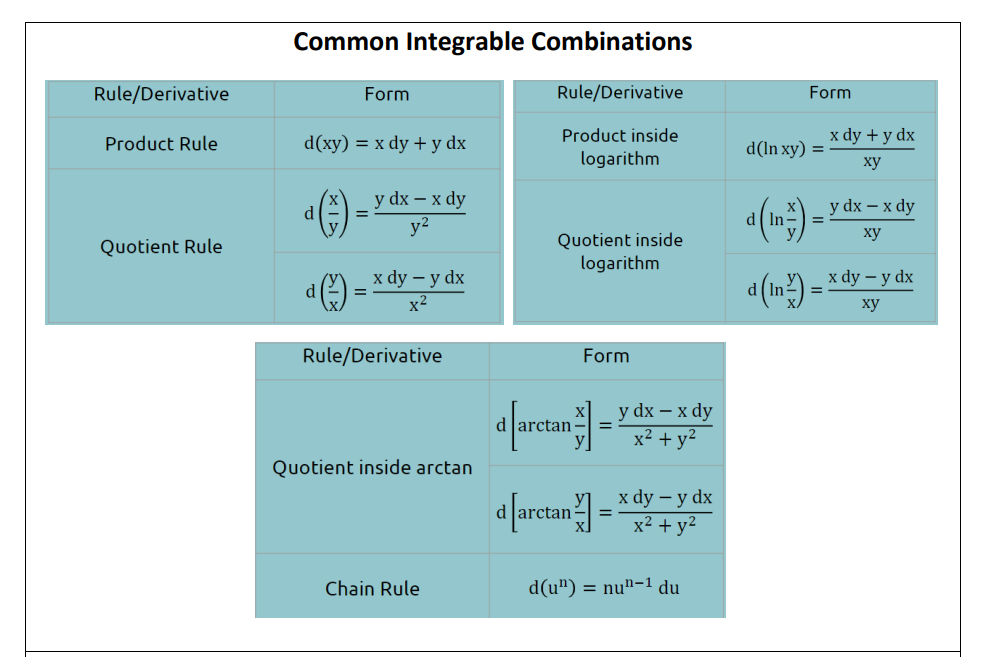
Question: DIFFERENTIAL EQUATION: INTEGRABALE COMBINATIONS Show straightforward, complete, and neat solution. Box final answer. Common Integrable Combinations Rule/Derivative Form Rule/Derivative Form Product Rule d(xy) = x
DIFFERENTIAL EQUATION: INTEGRABALE COMBINATIONS
Show straightforward, complete, and neat solution. Box final answer.

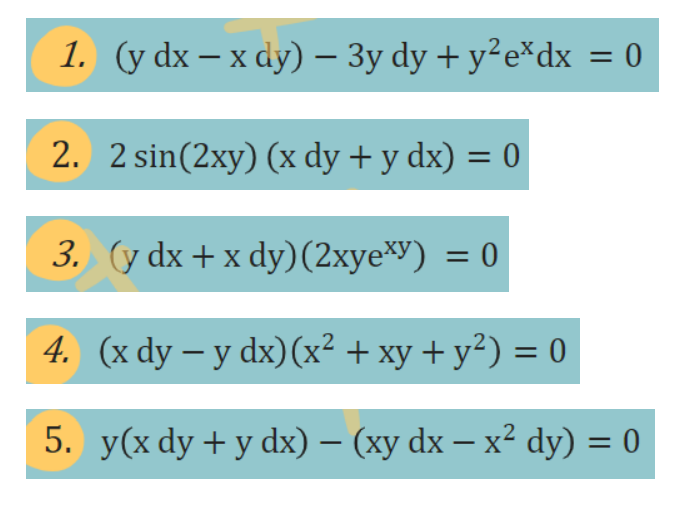
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


