Discrete Math

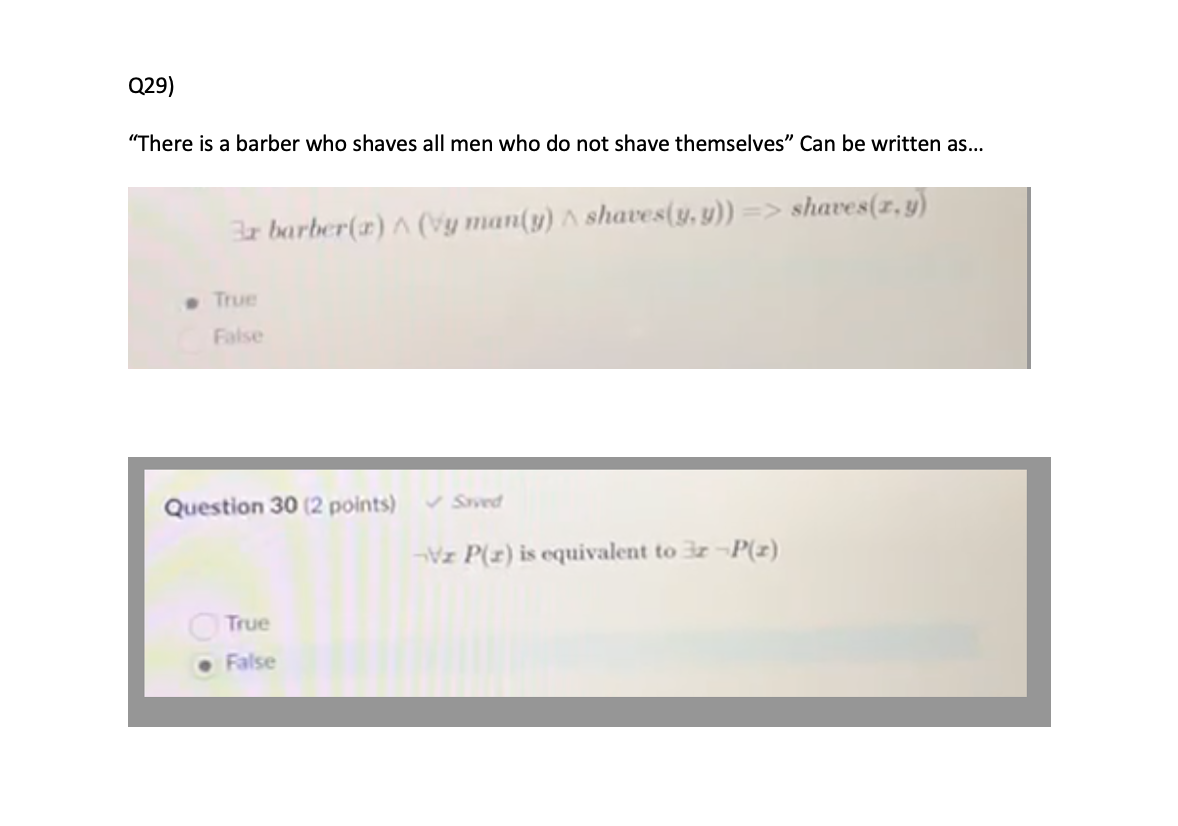
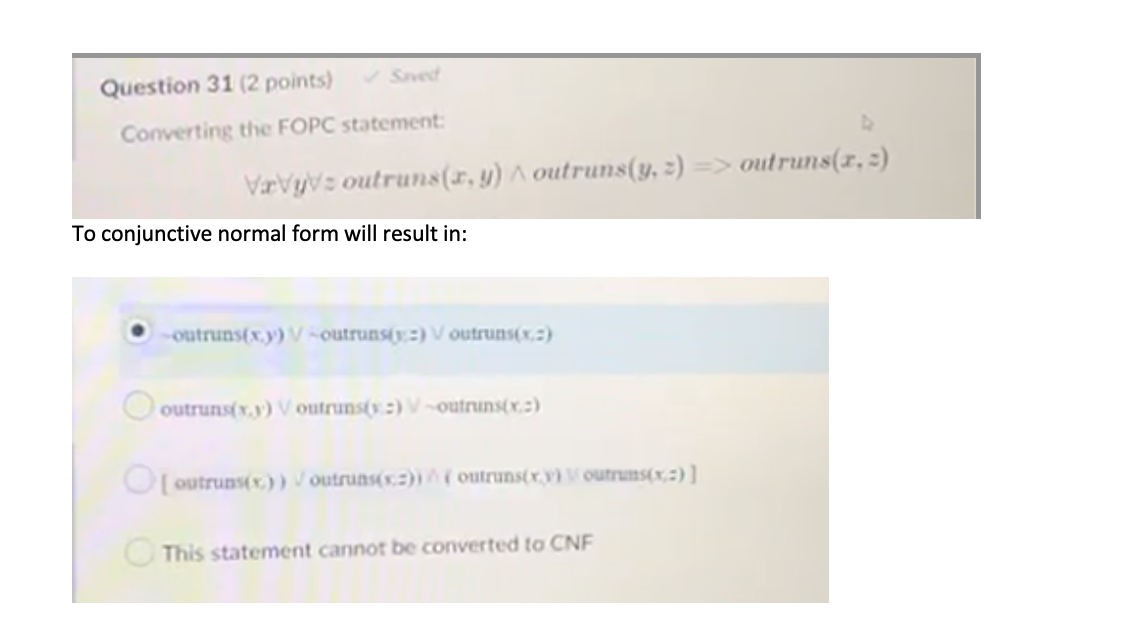
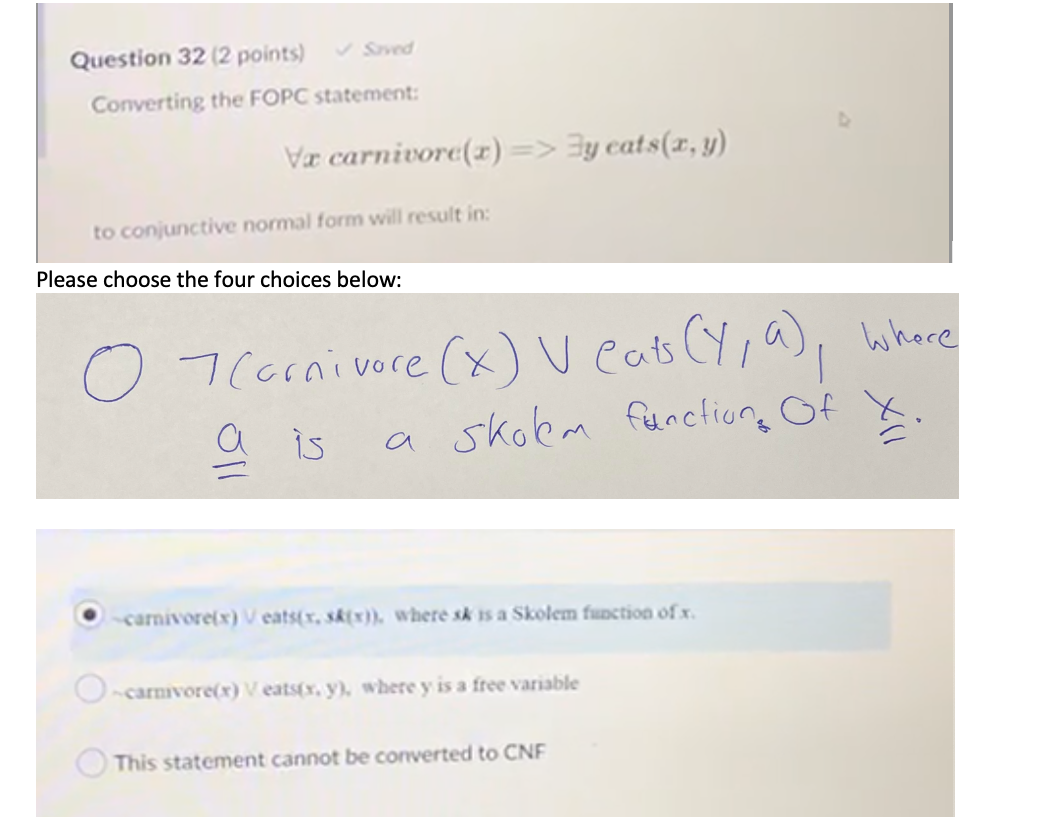
Q26: Given propositional variables, "Fire", "Smoke", and "Heat". Which of the following propositional logic statements are valid?(Select all that apply) Smoke => Smoke (Smoke \\/ Fire \\/ -Fire) (Smoke /\\ Fire) => Heat [ (Smoke /\\ Heat) => Fire) ((Smoke => Fire) \\/ (Heat => Fire)) Q27) "You can fool some of the people all of the time" can be written as... Vr (person(2) => time(t) A can fool(x, t)). True . False Question 28 (2 points) ~ Saved "You can fool all of the people some of the time" can be written as_. Ve(person(x) => It(time(t) A can fool(z,t))). . True False0.29} "There is a barber who shaves all men who do not shave themselves\" Can be written as... \fQuestion 32 (2 points) Saved Converting the FOPG statement: D Va carnivore(x) => By cats(x, y) to conjunctive normal form will result in: Please choose the four choices below: 7 Carnivore ( x ) V eats ( Y, a ), where a is a skolem functions Of X. -carnivore(x) V eats(x. sk(x)). where sk is a Skolem function of x. O-carnivore(x) V eats(x. y). where y is a free variable This statement cannot be converted to CNFQuestion 33 (2 points) Suppose that we have been given the following knowledge-base in clause form (x. y. z are variables and dog. lion, and zebra are constants: "-" represents the negation symbol): 1 ) Teats ( x , y ) V outruns ( xry) 2) Toutruns ( x ,g ) V y outruns ( y , z ) V Outruns ( x, 2 ) 3) eats (Lion, Zebra) 4 ) Outruns (zebra , dog) Mrace To prove Outruns(zebra, dog) using resolution-refutation, we begin with the negated goal "outruns(zebra, dog). Resolving this goal with clause 1 ..(Select all that apply). results in a subgoal: -eats(zebra, dog). Owill lead to a failed proof in the next step. will lead to a contradiction (empty clause) in the next step thus proving the original statement outruns(zebra, dog). is not possible because the goal does not resolve with clause 1