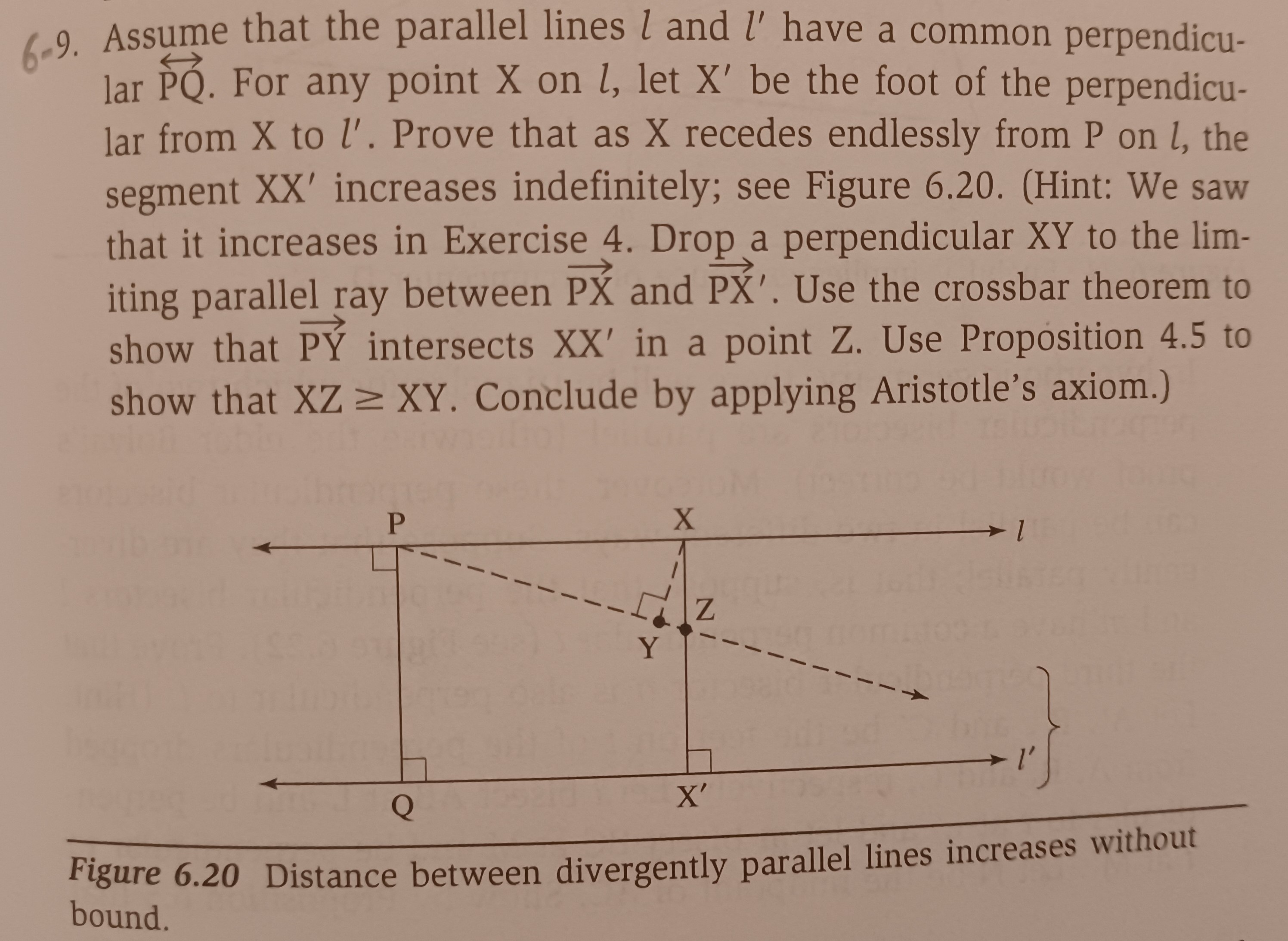
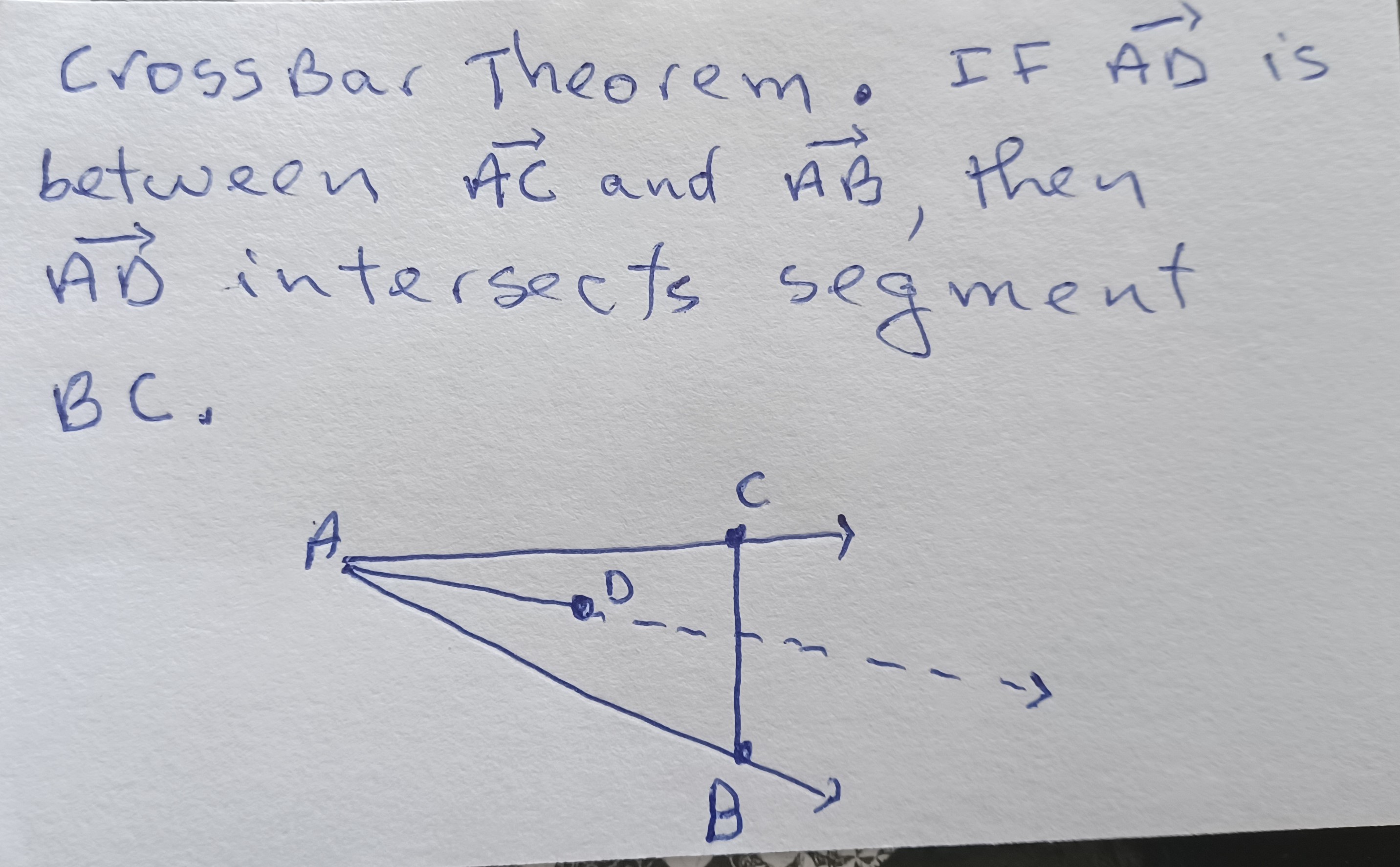
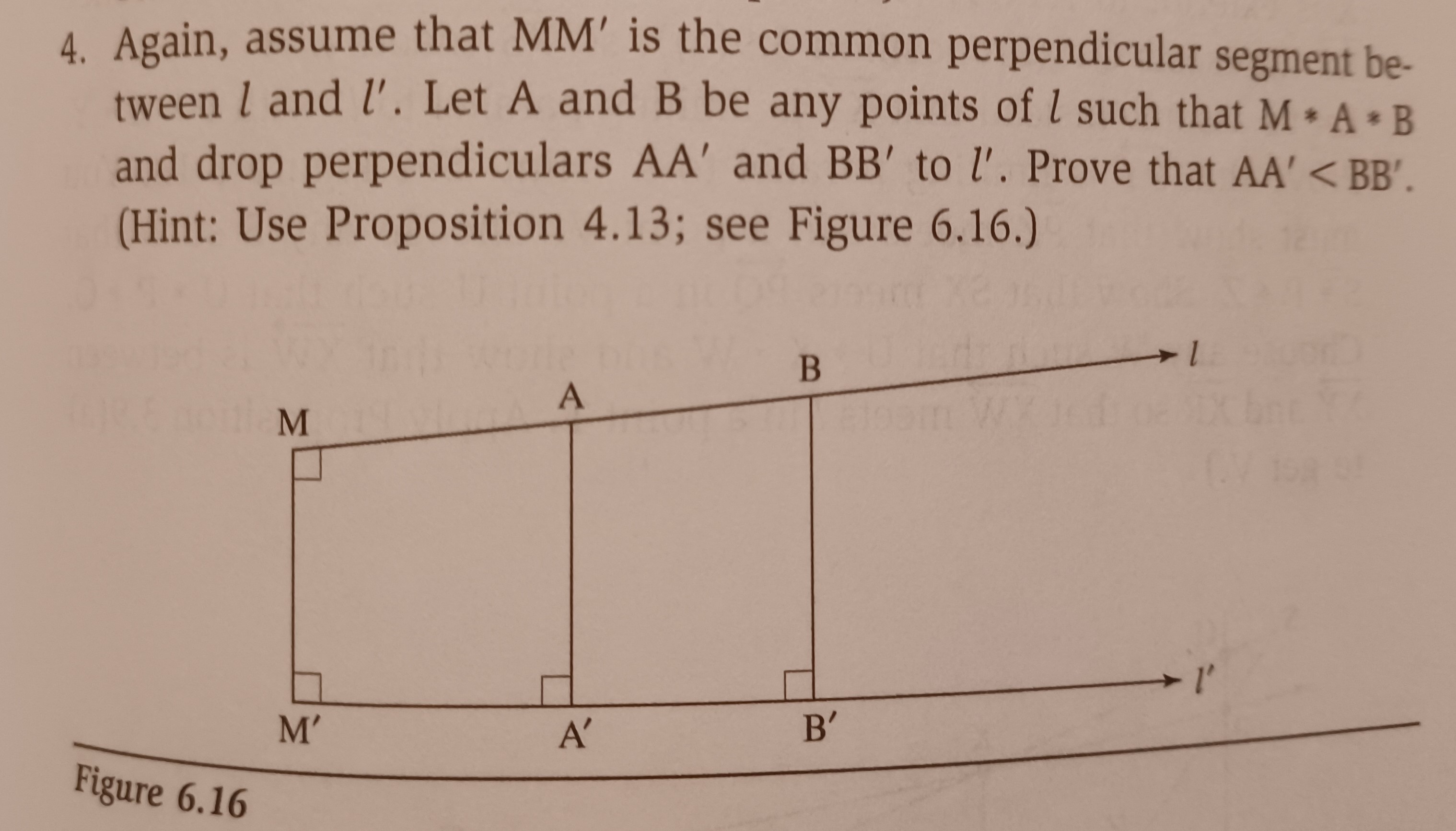
Question: do exercise 6:9 i added everything you might need to do it. like crossbar, aristotle, prop4.5, exercise 4. etc. let the real expert do it
"do exercise 6:9 i added everything you might need to do it. like crossbar, aristotle, prop4.5, exercise 4. etc. let the real expert do it"


Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


