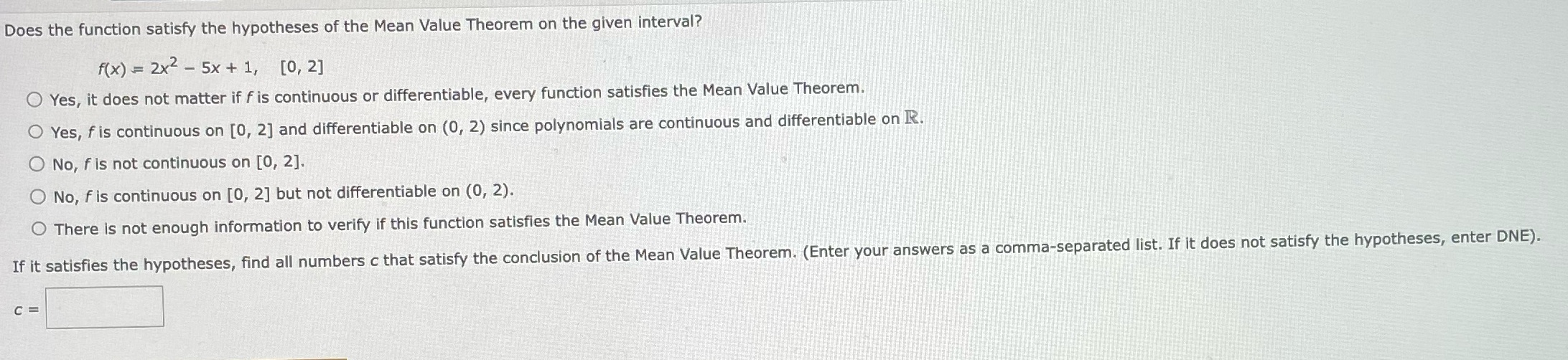
Question: Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? f(x) = 2x2 - 5x +1, [0, 2] Yes, it
![on the given interval? f(x) = 2x2 - 5x +1, [0, 2]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66661425ec043_86166661425ca46c.jpg)
Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? f(x) = 2x2 - 5x +1, [0, 2] Yes, it does not matter if f is continuous or differentiable, every function satisfies the Mean Value Theorem. Yes, f is continuous on [0, 2] and differentiable on (0, 2) since polynomials are continuous and differentiable on R. O No, f is not continuous on [0, 2]. O No, f is continuous on [0, 2] but not differentiable on (0, 2). O There is not enough information to verify if this function satisfies the Mean Value Theorem. If it satisfies the hypotheses, find all numbers c that satisfy the conclusion of the Mean Value Theorem. (Enter your answers as a comma-separated list. If it does not satisfy the hypotheses, enter DNE)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


