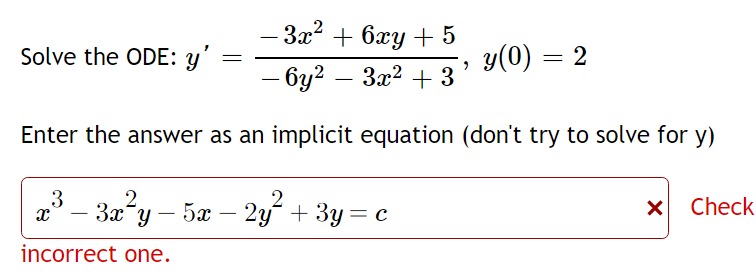
dy Consider the differential equation dt = 6y(y - 1) (y - 3). Use a phase-line analysis to determine whether each of the following equilibrium solutions are stable or unstable. The equilibrium solution y = 0 is: O Unstable O Half-stable O Stable The equilibrium solution y = 1 is: O Half-stable O Unstable O Stable X The equilibrium solution y = 3 is: O Unstable O Stabledy 3y The general solution of the ODE e is: dt t y ( t ) = t,3 et + C X Use C for any undetermined constant in your answer.A tank contains 60 kg of salt and 2000 L of water. Pure water enters a tank at the rate 8 Limin. The solution is mixed and drains from the tank at the rate 10 L! min. Let y be the number of kg of salt in the tank after 15 minutes. The differential equation for this situation would be: 3_ 3g dt t500 x y(0) =[ 0.03 \"l -3x2 + 6xy + 5 Solve the ODE: y' = -6y2 - 3x2 + 3' 3(0) = 2 Enter the answer as an implicit equation (don't try to solve for y) 2 - 3xy - 5x - 2y + 3y = c X Check incorrect one.Biologists stocked a lake with 300 fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be 3800. The number of fish doubled in the first year. (a) Assuming that the size of the fish population satisfies the logistic equation dP P =kP 1 dt ( K)' determine the constant k, and then solve the equation to find an expression for the size of the population after t years. 114008078315 35 + sell-783* P(t) : (b) How long will it take for the population to increase to 1900 (half of the carrying capacity)? It will take years