Dynamic Programming

When solving the question, can you explain all the steps in detail? I mean, can you show me all 4 steps when solving the question? I wrote the steps below. Pseudocode should be in C. Also, a bottom-up approach must be used not memoization. It is a bit urgent.

Steps:

1. Characterize the structure of an optimal solution.

2. Recursively define the value of an optimal solution.

3. Compute the value of an optimal solution, typically in a bottom-up fashion.

4. Construct an optimal solution from computed information.

Also, there is one more question which is related to this question. I am attaching it to below:

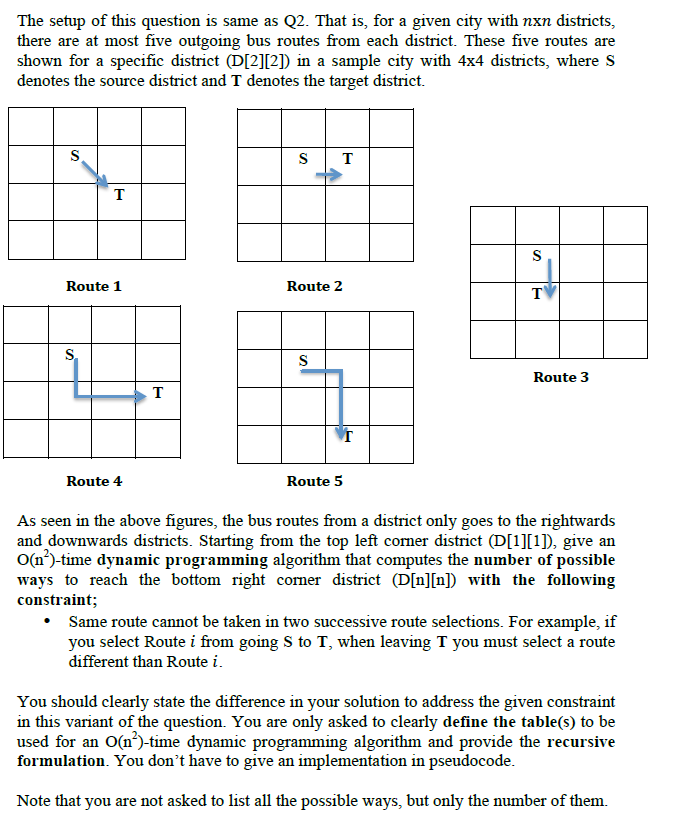
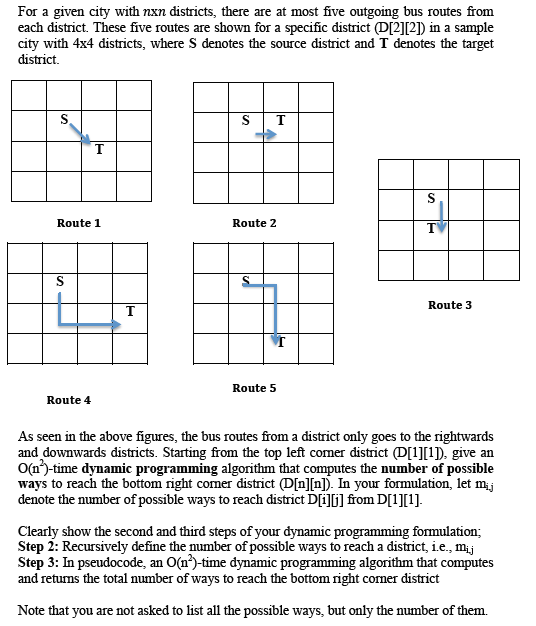
For a given city with nxn districts, there are at most five outgoing bus routes from each district. These five routes are shown for a specific district (D[2][2]) in a sample city with 4x4 districts, where S denotes the source district and I denotes the target district S T T S Route 1 Route 2 T T Route 3 1 Route 5 Route 4 As seen in the above figures, the bus routes from a district only goes to the rightwards and downwards districts. Starting from the top left comer district (D[1][1], give an 0(1)-time dynamic programming algorithm that computes the number of possible ways to reach the bottom right comer district (D[n][n]). In your formulation, let mij denote the number of possible ways to reach district D[i][] from D[1][1]. Clearly show the second and third steps of your dynamic programming formulation; Step 2: Recursively define the number of possible ways to reach a district, i.e., mij Step 3: In pseudocode, an O(n)-time dynamic programming algorithm that computes and returns the total number of ways to reach the bottom right corner district Note that you are not asked to list all the possible ways, but only the number of them. The setup of this question is same as Q2. That is, for a given city with nxn districts, there are at most five outgoing bus routes from each district. These five routes are shown for a specific district (D[2][2]) in a sample city with 4x4 districts, where S denotes the source district and T denotes the target district. s ST T S Route 1 Route 2 T S S Route 3 T Route 4 Route 5 As seen in the above figures, the bus routes from a district only goes to the rightwards and downwards districts. Starting from the top left corner district (D[1][1], give an O(n)-time dynamic programming algorithm that computes the number of possible ways to reach the bottom right comer district (D[n][n]) with the following constraint; Same route cannot be taken in two successive route selections. For example, if you select Route i from going S to T, when leaving T you must select a route different than Route i. You should clearly state the difference in your solution to address the given constraint in this variant of the question. You are only asked to clearly define the table(s) to be used for an O(n)-time dynamic programming algorithm and provide the recursive formulation. You don't have to give an implementation in pseudocode. Note that you are not asked to list all the possible ways, but only the number of them