EASY DYNAMIC PROGRAMMING OPTIMAL BINARY TREE

This question concerns the dynamic programming algorithm for computing a binary tree, discussed in class in and in the notes. Suppose we are given the following data, consisting of 8 key values and the frequency with which each key is accessed:

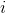	Data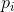
1	A	0.09
2	B	0.17
3	C	0.26
4	D	0.05
5	E	0.06
6	F	0.12
7	G	0.10
8	H	0.15

(a) For each i and j in the appropriate range, give the values of E[i, j] and root[i, j].

(b) Draw the optimal binary tree for the data given above.

(c) What is the weighted lookup cost of the optimal binary tree? Explain briefly how you computed it.

Transcribed image text