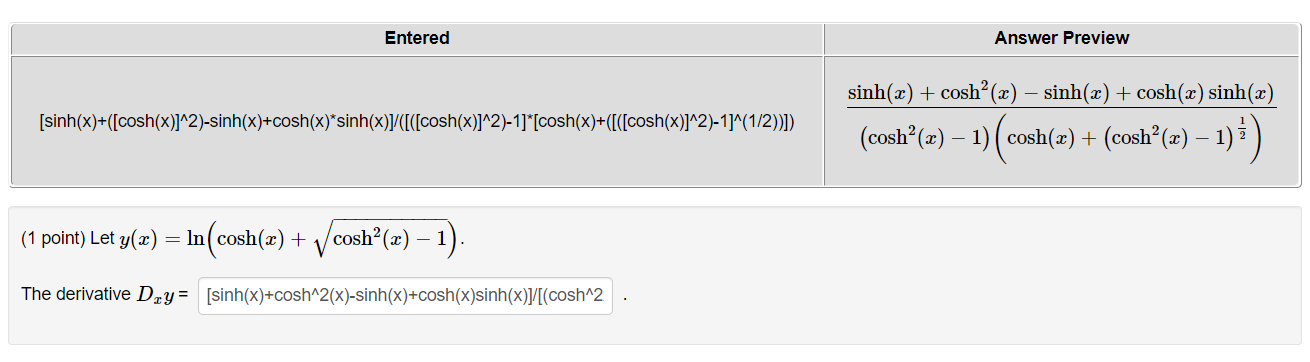
Question: Entered Answer Preview sinh(a) + cosh (x) - sinh(x) + cosh(x) sinh(x) [sinh(x)+([cosh(x)]^2)-sinh(x)+cosh(x)sinh(x)]/([([cosh(x)]^2)-1][cosh(x)+([([cosh(x)]^2)-1]^(1/2))]) (cosh?(x) - 1) cosh(a) + (cosh?(x) - 1) ? (1 point) Let

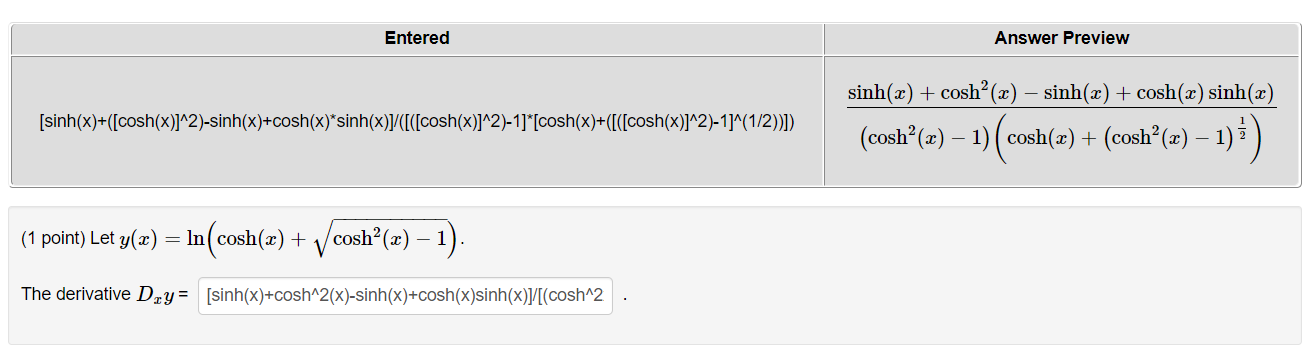
point) Let y(x) = In cosh(x) + cosh?(x) - 1) The derivative

Dry = [sinh(x)+cosh^2(x)-sinh(x)+cosh(x)sinh(x)]/[(cosh^2(1 point) Use sigma notation to write the Maclaurin series

Entered Answer Preview sinh(a) + cosh (x) - sinh(x) + cosh(x) sinh(x) [sinh(x)+([cosh(x)]^2)-sinh(x)+cosh(x)*sinh(x)]/([([cosh(x)]^2)-1]*[cosh(x)+([([cosh(x)]^2)-1]^(1/2))]) (cosh?(x) - 1) cosh(a) + (cosh?(x) - 1) ? (1 point) Let y(x) = In cosh(x) + cosh?(x) - 1) The derivative Dry = [sinh(x)+cosh^2(x)-sinh(x)+cosh(x)sinh(x)]/[(cosh^2(1 point) Use sigma notation to write the Maclaurin series for the function. ]n(7 + x). (Note rst term separate and summation from k 1)1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The given example in the image I uploaded should be the format of the solution.[Type the ANSWERS and SOLUTIONS electronically with your devices] Differentiation of Hyperbolic Functions The...

Symbolic answers must be entered using notation similar to the examples given below. If you enter decimal numbers for questions that indicate that a symbolic answer is required, it will be marked as...

7/4/23, 11:16 PM Homework 8.7-Anh Nguyen Use a table of integrals to determine tv7t+ 19 at. Click here to view page 1 of the integral table. " Click here to view page 2 of the integral table. 14...

Part 1: Boosts and rapidity For this part, we will need the definitions of the hyperbolic trig functions, sinh (pronounced "sinsh"), cosh (pronounced like it sounds), and tanh (pronounced "tansh"):...

= n a X 2 n 2 2 EnE 2 ma3. ( /24 pts) Suppose an infinite square well potential is given by c D (a) (4 pts) Sketch the potential. (b) (12 pts) As we saw in class, the general solution to the infinite...

5. /16 pts) A particle in a one-dimensional, infinite square well of length L has the initial, normalized wave function CO I (x, 0) = (a) (8 pts) Find I(x, t). (b) (4 pts) What is the probability of...

EXERCISES 7.7 Values and Identities 9. (sinh x + cosh x)4 Each of Exercises 1-4 gives a value of sinh x or cosh x. Use the defi- 10. In (cosh x + sinh x) + In (cosh x - sinh x) nitions and the...

wall A ladder 10 ft long rests against a vertical wall. If the bottom of the lad- der slides away from the wall at a rate of I ft/s, how fast is the top of the ladder sliding down the wall when the...

4. ( function /30 pts) This problem must be done without online integrators. A particle has the wave Y(x) = { Axe-Ax 0 0

Functions involving certain combinations of e* and ex occur so frequently in applied mathematics that they warrant special study. These functions, called the hyperbolic functions, have properties...

Study Appendix 16A. Kalitzki Implements Company had sales revenue of $710,000 in 20X2. Pertinent data for its only product in 20X2 included the following: 1. Prepare a statement of gross margin for...

A shallow-water wave 12 cm high propagates into still water of depth 1.1 m. Compute (a) The wave speed; and (b) The induced velocity V.

Consider the nonhomogeneous ODE, y ' ' a 1 y ' a 0 y = 4 l n ( t ) e - 3 t The homogeneous solution is , y 1 ( t ) = c 1 e - 3 t c 2 t e - 3 t The particular solution is , y p ( t ) =

Identify the factors that an entrepreneur should consider when selecting an organizational form for a business.

You have been given the following information for Moores HoneyBee Corp.: a. Net sales = $32,000,000; b. Gross profits = $18,700,000; c. Other operating expenses = $2,500,000; d. Addition to retained...

Metropolitan Research, Inc., a consumer research organization, conducts surveys designed to evaluate a wide variety of products and services available to consumers. In one particular study,...

A person can just see the print in a book clearly when she holds the book no closer than at arms length (0.45 m from the eyes). (a) Does she have (1) nearsightedness, (2) farsightedness, or (3)...

A person 1.20 km away from you fires a gun. A wind is blowing at 10.0 m/s. How much different from the no wind time of travel is there for the sound to reach you compared to the situation when the...

plz help Question 14 Not yet answered Points out of 1 P Flag question Dash line on an arrow diagram represent "dummy activities". Select one: True False Not yet answered Question 15 Points out of 1...

8. What are the costs of collecting the information?

6. How great is the time-lag between when an event occurs until we get information about it?

1. Build trust and share information with others.

Question: Entered Answer Preview sinh(a) + cosh (x) - sinh(x) + cosh(x) sinh(x) [sinh(x)+([cosh(x)]^2)-sinh(x)+cosh(x)*sinh(x)]/([([cosh(x)]^2)-1]*[cosh(x)+([([cosh(x)]^2)-1]^(1/2))]) (cosh?(x) - 1) cosh(a) + (cosh?(x) - 1) ? (1 point) Let

Step by Step Solution

Students Have Also Explored These Related Mathematics Questions!

Question: Entered Answer Preview sinh(a) + cosh (x) - sinh(x) + cosh(x) sinh(x) [sinh(x)+([cosh(x)]^2)-sinh(x)+cosh(x)sinh(x)]/([([cosh(x)]^2)-1][cosh(x)+([([cosh(x)]^2)-1]^(1/2))]) (cosh?(x) - 1) cosh(a) + (cosh?(x) - 1) ? (1 point) Let