Estimate the sine function using an accelerated Maclaurin series

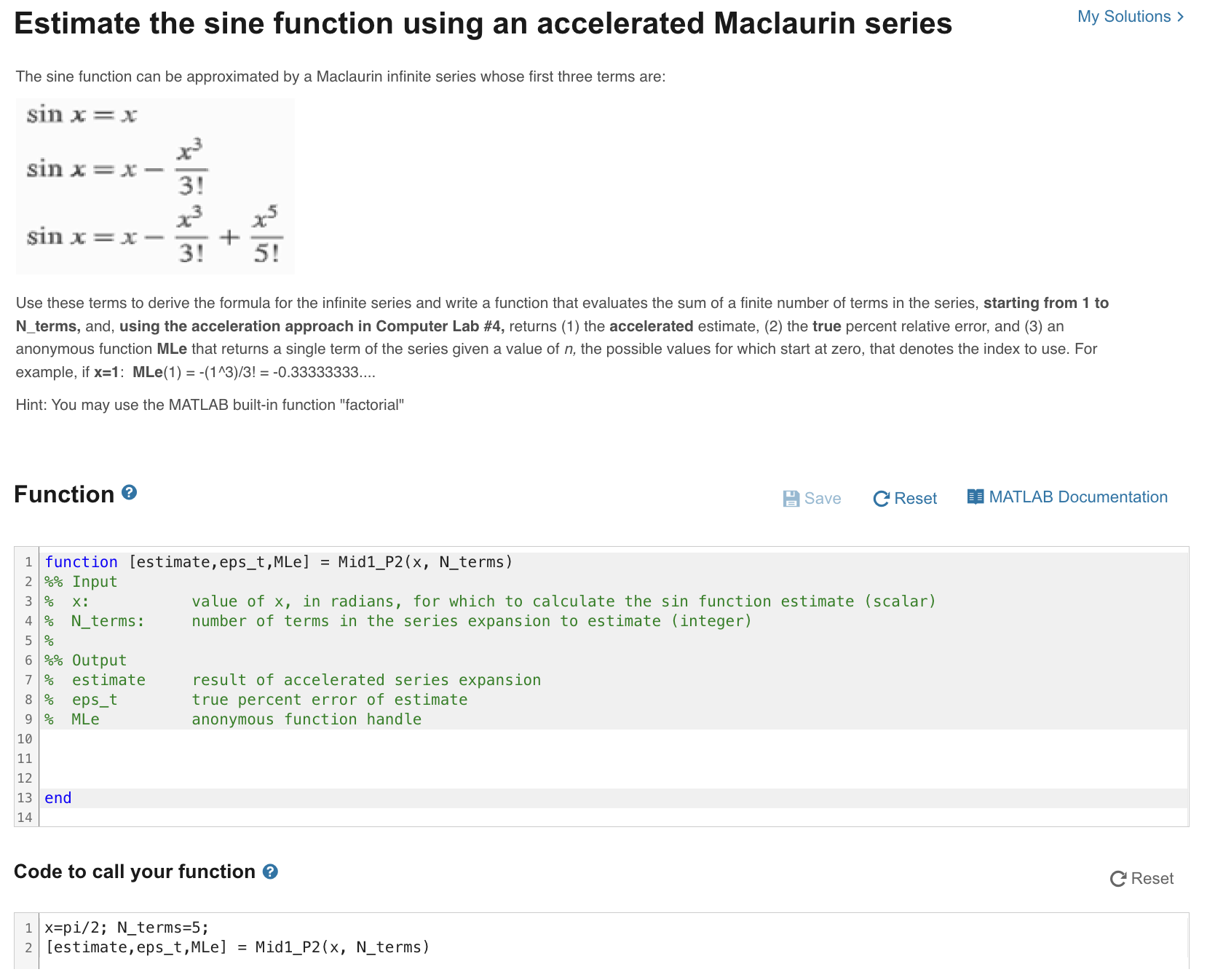
The sine function can be approximated by a Maclaurin infinite series whose first three terms are:

Use these terms to derive the formula for the infinite series and write a function that evaluates the sum of a finite number of terms in the series, starting from $1$ to

N$\_$terms, and, using the acceleration approach in Computer Lab #$4,$ returns $(1)$ the accelerated estimate, $(2)$ the true percent relative error, and $(3)$ an

anonymous function MLe that returns a single term of the series given a value of $n,$ the possible values for which start at zero, that denotes the index to use. For

example, if $x=1$ : MLe$(1)=-\frac{1^{{?}^{{?}^{?}}}3}{3}-0\mathrm{.}33333333$dots

Hint: You may use the MATLAB built$-$in function "factorial"

Function $($

function $[$estimate$,$ eps$\_$t$,$MLe$]=$ Mid$1\_$P$2($x$,$ N$\_$terms$)$

$\%$ Input

$\%$ x: value of $x,$ in radians, for which to calculate the sin function estimate $($scalar$)$

$\%$ N$\_$terms: number of terms in the series expansion to estimate $($integer$)$

$\%$

$\%$ Output

$\%$ estimate result of accelerated series expansion

$\%$ eps$\_$t true percent error of estimate

$\%$ MLe anonymous function handle

end

Code to call your function $?$

$x=\frac{}{2}$; N$\_$terms$=5$;

$[$estimate$,$ eps$\_$t$,$MLe$]=$ Mid$1\_$P$2($x$,$ N$\_$terms$)$