Question: EXAMPLE 1 Let -2 0 -17 r1 = (-2, -5, 8,0, -17) 1 3 - 5 12 = (1,3, -5, 1, 5) A = and

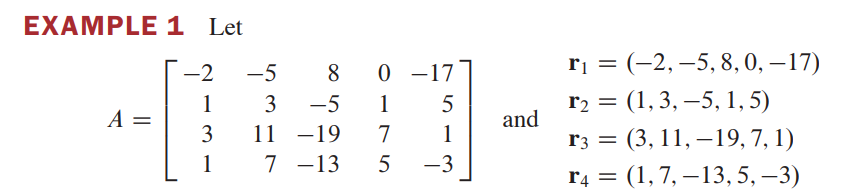
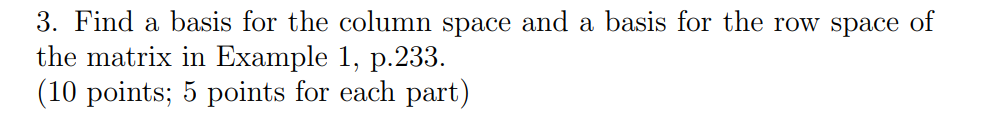
EXAMPLE 1 Let -2 0 -17 r1 = (-2, -5, 8,0, -17) 1 3 - 5 12 = (1,3, -5, 1, 5) A = and 3 11 -19 7 r3 = (3, 1 1, -19, 7, 1) 7 -13 5 r4 = (1,7, -13, 5, -3)3. Find a basis for the column space and a basis for the row space of the matrix in Example 1, p.233. (10 points; 5 points for each part)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Score 80 73 81 78 88 79 77 84 62 70 69 75 84 77 75 71 65 79 68 85 74 52 70 77 84 Employee 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39...

please help with the following: include the Microsoft Project File along with a memo thank you and answer part 3 questions: Red Zuma Project Part 3 Come of the Red Zone intor Wichis locaten Anped the...

PLEASE help me answer these questions using the information below Please use the Activity ID Numbers Letters described in the case and NOT what the software assigns (if different). Part 1: 1. The...

1. You are managing the project of planning a party for your company employees. There is a risk that the employees will not come to the party. You decide to not take any action against this as the...

6. E-mail messages sent over the Internet are broken up into electronic packets that may take a variety of different paths to reach their destination where the original message is reassembled....

Write a function blockcount for the Shell class int Shell::blockcount(string file) which accepts a file name "file" and returns the number of blocks used by that file. Note this function can be used...

The following questions refer to the following information Initial State: Translation Look Aside Buffer Valid Tag Physical Page Number Age 1 11 12 10 2 4 20 "Age" refers to the number of clock cycles...

Write an assembler in Python (Comment Heavily) that reads the source code of an assembly program (for an imaginary machine) and displays the machine language for that program. The following assembler...

Write an assembler in Jsva (Comment Heavily) that reads the source code of an assembly program (for an imaginary machine) and displays the machine language for that program. The following assembler...

Exponential Probabilities Mean Lambda 8000 0.000125 x F(x) 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 11000 12000 13000 14000 15000 16000 17000 18000 19000 20000 21000 22000 23000 24000...

The balance sheet data of Wheels n Tires, Inc. at the end of 2014 and 2013 follow. Equipment was purchased for $21,000 in exchange for common stock, par $21,000, during the year; all other equipment...

Fill in the sheet titled NPV-IRR. Lydia will buy the property in 2014, she will collect NOI for 5 years 2015-2019, and she will sell it in 2019. Lydias loan has a 5/4/3/2/1 prepayment penalty...

Why is inventory treated differently than property, plant, and equipment when classifying their cash effects on the statement of cash flows? ( Select all that apply. ) Multiple select question....

A commitee has started selling gluten free cigars and chewing tobacco from a joint process involving the processing of tobacco leaves. Joint costs are $60,000 for this process and yields 2000 pounds...