Example

PROBLEM

I post the example, please solve the real problem

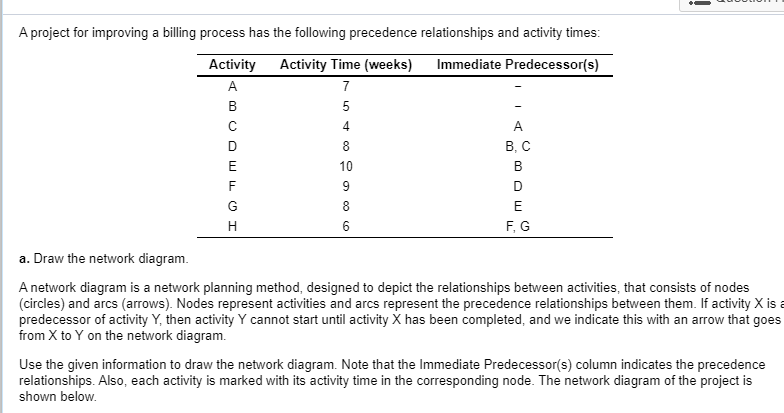
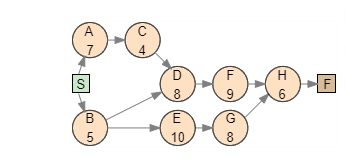
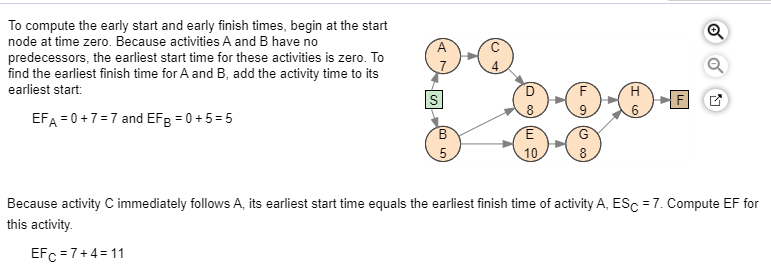
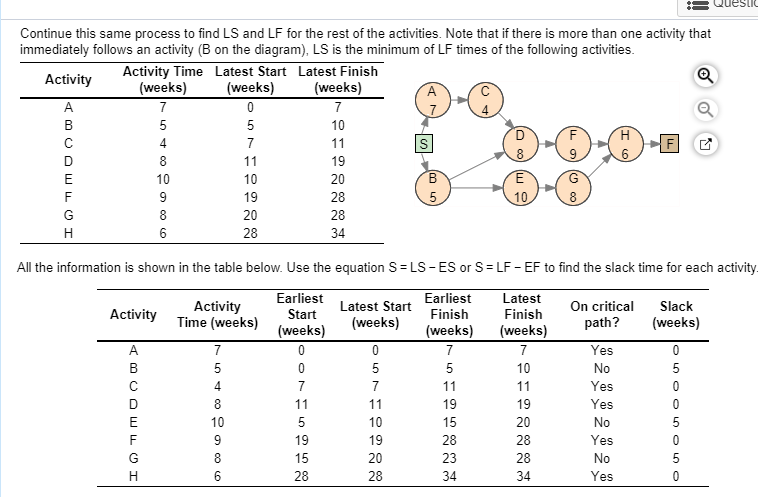
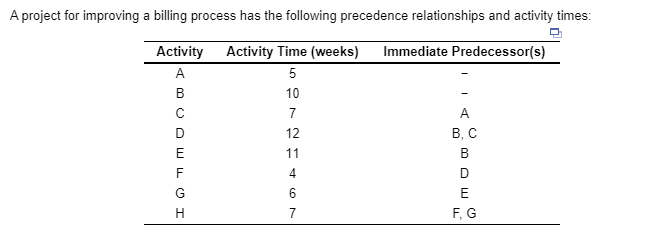
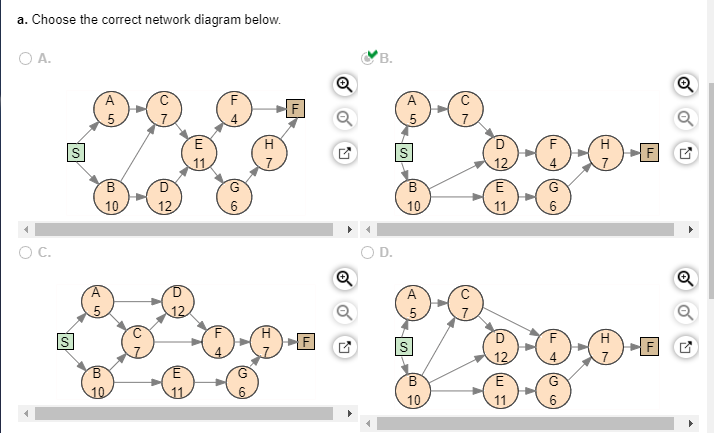
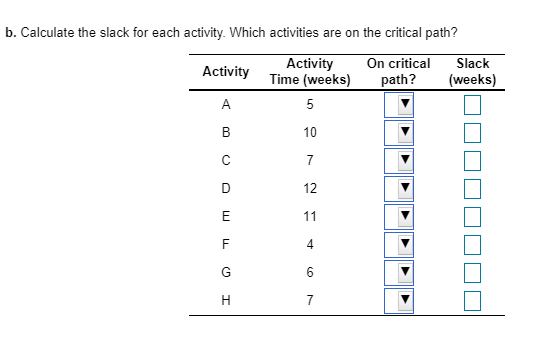
A project for improving a billing process has the following precedence relationships and activity times: Activity Activity Time (weeks) Immediate Predecessor(s) B, C MOOWLUI a. Draw the network diagram. A network diagram is a network planning method, designed to depict the relationships between activities, that consists of nodes (circles) and arcs (arrows). Nodes represent activities and arcs represent the precedence relationships between them. If activity X is a predecessor of activity Y, then activity Y cannot start until activity X has been completed, and we indicate this with an arrow that goes from X to Y on the network diagram. Use the given information to draw the network diagram. Note that the Immediate Predecessor(s) column indicates the precedence relationships. Also, each activity is marked with its activity time in the corresponding node. The network diagram of the project is shown below. b. Calculate the slack for each activity. Which activities are on the critical path? The maximum length of time that an activity can be delayed without delaying the entire project is called activity slack. Consequently, activities on the critical path have zero slack. Activity slack can be calculated in one of two ways for any activity: SELS-ES or S=LF-EF, where S represents the slack, LS is the activity's latest start time, ES is the activity's earliest start time, LF is the activity's latest finish time, and EF is the activity's earliest finish time. The earliest start and earliest finish times are obtained as follows: 1. The earliest finish time (EF) of an activity equals its earliest start time plus its estimated duration, t, or EF = ES +t. 2. The earliest start time (ES) for an activity is the earliest finish time of the immediately preceding activity. For activities with more than one preceding activity, ES is the maximum of the earliest finish times of the preceding activities. To obtain the latest start and latest finish times, we must work backward from the finish node. We start by setting the latest finish time of the project equal to the earliest finish time of the last activity on the critical path. 1. The latest finish time (LF) for an activity is the latest start time of the activity that immediately follows. For activities with more than one activity that immediately follow, LF is the minimum of the latest start times of those activities. 2. The latest start time (LS) for an activity equals its latest finish time minus its estimated duration, t, or LS = LF-t. To compute the early start and early finish times, begin at the start node at time zero. Because activities A and B have no predecessors, the earliest start time for these activities is zero. To find the earliest finish time for A and B, add the activity time to its earliest start: EFA = 0 + 7 = 7 and EFB = 0 + 5 = 5 Because activity C immediately follows A, its earliest start time equals the earliest finish time of activity A, ESC = 7. Compute EF for this activity EFC = 7+4 = 11 Continue this same process to find ES and EF for the rest of the activities. Note that if there is more than one preceding activity (D and H on the diagram), ES is the maximum of EF times of the preceding activities. Activity Time Earliest Start Earliest Finish Activity (weeks) (weeks) (weeks) + coco To obtain the latest start and latest finish times, we must work backward from the finish node. Start by setting the latest finish time of the project equal to the earliest finish time of the last activity on the critical path. So, the latest finish time of activity H is the earliest finish time of this activity, which is 34 weeks. Compute the latest start time for this activity by subtracting the activity time. LSH = 34 - 6 = 28 The LF time for the activities F and G is the LS time of H, which is the only activity that follows them. LFG=LFF = LSH = 28 Find the LS times for each of the activities F and G. LSG = 28 -8 = 20 and LSF = 28- 9 = 19 3 Queste Continue this same process to find LS and LF for the rest of the activities. Note that if there is more than one activity that immediately follows an activity (B on the diagram), LS is the minimum of LF times of the following activities. Activity Activity Time Latest Start Latest Finish (weeks) (weeks) (weeks) s Q-0-0-0 C IOTO All the information is shown in the table below. Use the equation S = LS-ES or S = LF - EF to find the slack time for each activity Earliest Latest Start Activity Earliest Latest Activity Finish Start Time (weeks) Finish On critical path? (weeks) Slack (weeks) (weeks) (weeks) (weeks) Yes No Yes IOTMOOD Yes No Yes No Yes A project for improving a billing process has the following precedence relationships and activity times: Activity Activity Time (weeks) Immediate Predecessor(s) COOWLUI LOCO F, G a. Choose the correct network diagram below. OA. OD. -0-0-0 b. Calculate the slack for each activity. Which activities are on the critical path? Activity Activity Time (weeks) Tin On critical path? Slack (weeks) Cow I 0000000