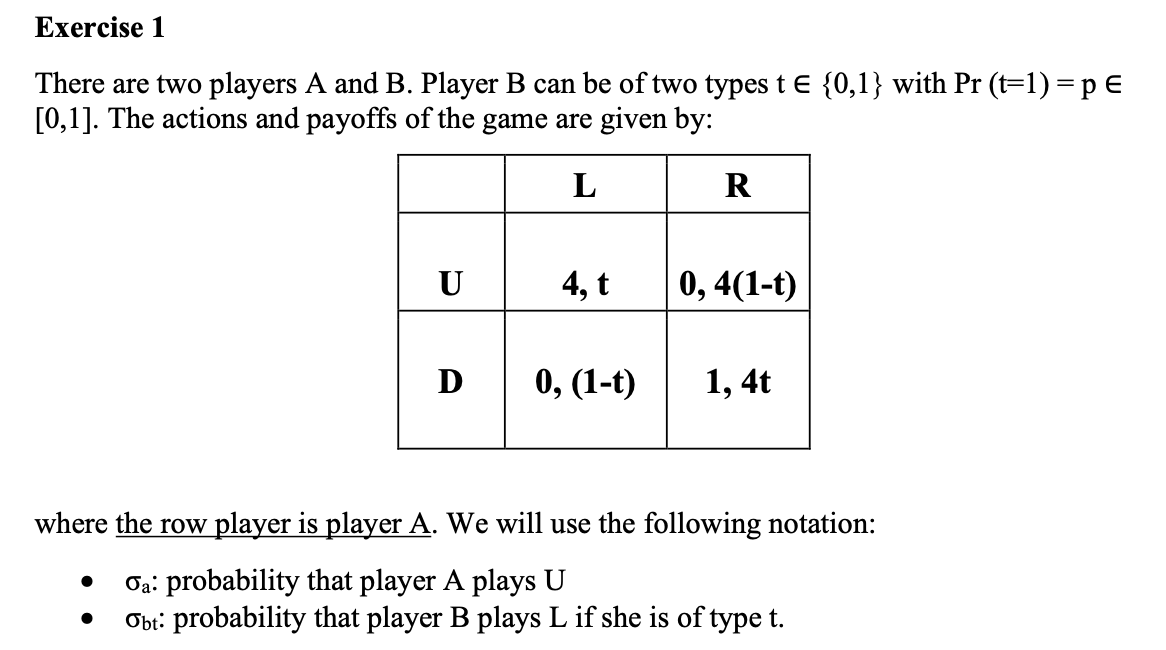
Question: Exercise 1 There are two players A and B. Player B can be of two types t E {0,1} with Pr (t=1) = p 6

![p 6 [0,1]. The actions and payoffs of the game are given](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66788d5373b97_53166788d535093f.jpg)
Exercise 1 There are two players A and B. Player B can be of two types t E {0,1} with Pr (t=1) = p 6 [0,1]. The actions and payoffs of the game are given by: where the row player is player A. We will use the following notation: 0 Ga: probability that player A plays U 0 obt: probability that player B plays L if she is of type t. Part II (5 marks): Incomplete information Suppose p = 0.5. Check whether the following strategy profiles constitute a BNE: (i) (Ca, Obl, Obo) = (1,1, 1) (ii) (Ca, Obl, Obo) = (0,0,0) (iii) (Oa, Obl, Ob0) = (1, 1,0) (iv) (Ca, Obl, Obo) = (0,0, 1) V (Oa, Obl, Obo) = (0.8,0.2,0.2) . To prove something is not a BNE, you need to show that just one of the three - type-0 player B, type-1 player B, or player A has an incentive to deviate. . To prove something is a BNE you have to check that no player-type has an incentive to deviate from the proposed strategy profile
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


