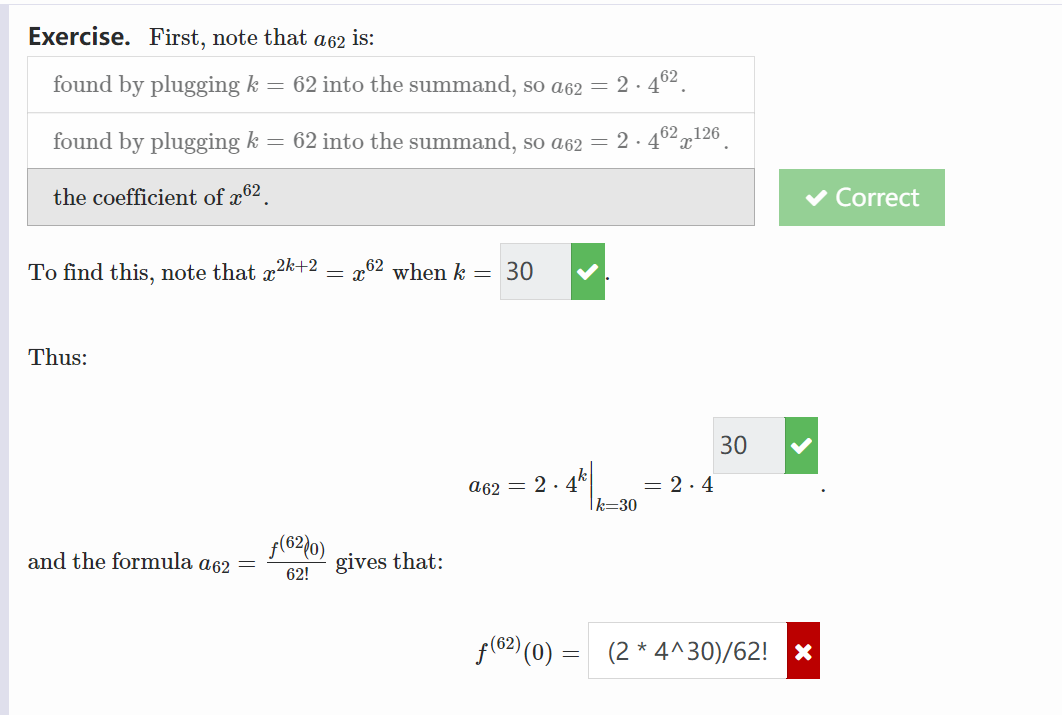
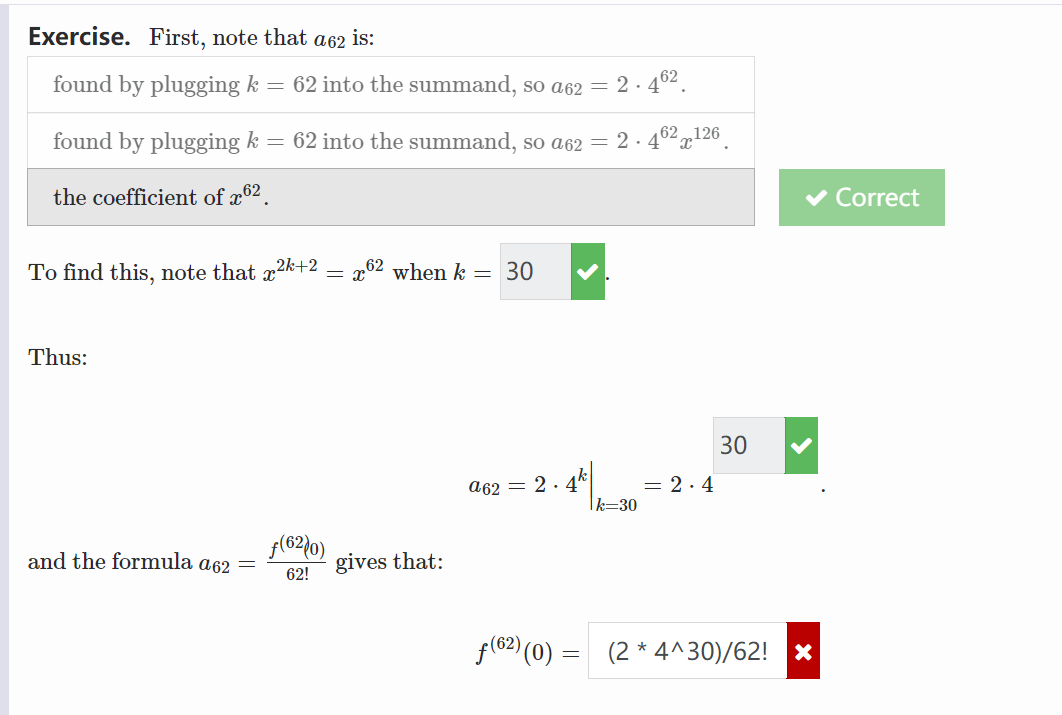
Exercise. For the function f(x) = sin(2x) + cos(3x), find the seventh degree Taylor polynomial centered at x = 0. The seventh degree Taylor polynomial is: P7 (2) = ?Exercise. Now, we can use the relationship that if f(x) = Croak(x - c), then an = f( (c) n! Here, c = 0 v , and to find f(62) (0), we have n = 62 We now need to find a62. Exercise. First, note that a62 is: found by plugging k = 62 into the summand, so a62 = 2 . 462. found by plugging k = 62 into the summand, so a62 = 2 . 462 2 126 the coefficient of a 62. Correct To find this, note that x2k+2 = x2 when k = 30 V Thus: 30 V a62 = 2 . 4k = 2 .4 k=30Exercise. First, note that a62 is: found by plugging k = 62 into the summand, so a62 = 2 . 462. found by plugging k = 62 into the summand, so a62 = 2 . 462-126 the coefficient of 2 62. Correct To find this, note that a2k+2 = x2 when k = 30 V Thus: 30 V a62 = 2 . 4k = 2 . 4 I k=30 and the formula a62 = f(620) 62! gives that: f (62) (0) = (2 * 4^30)/62! X