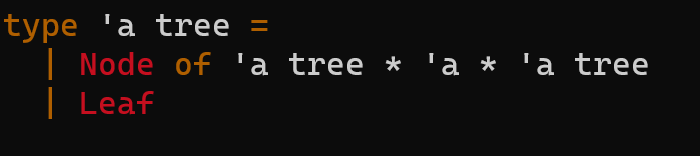
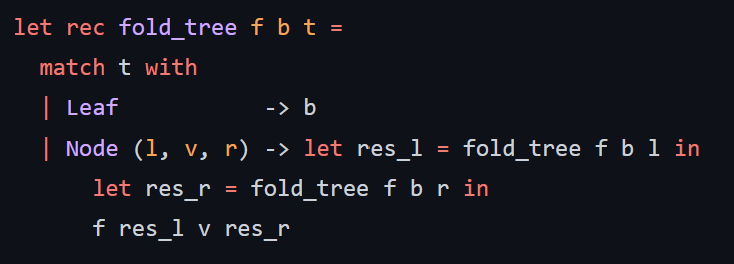
(f = function, b = accumulator, t = tree)

Please code in OCaml.

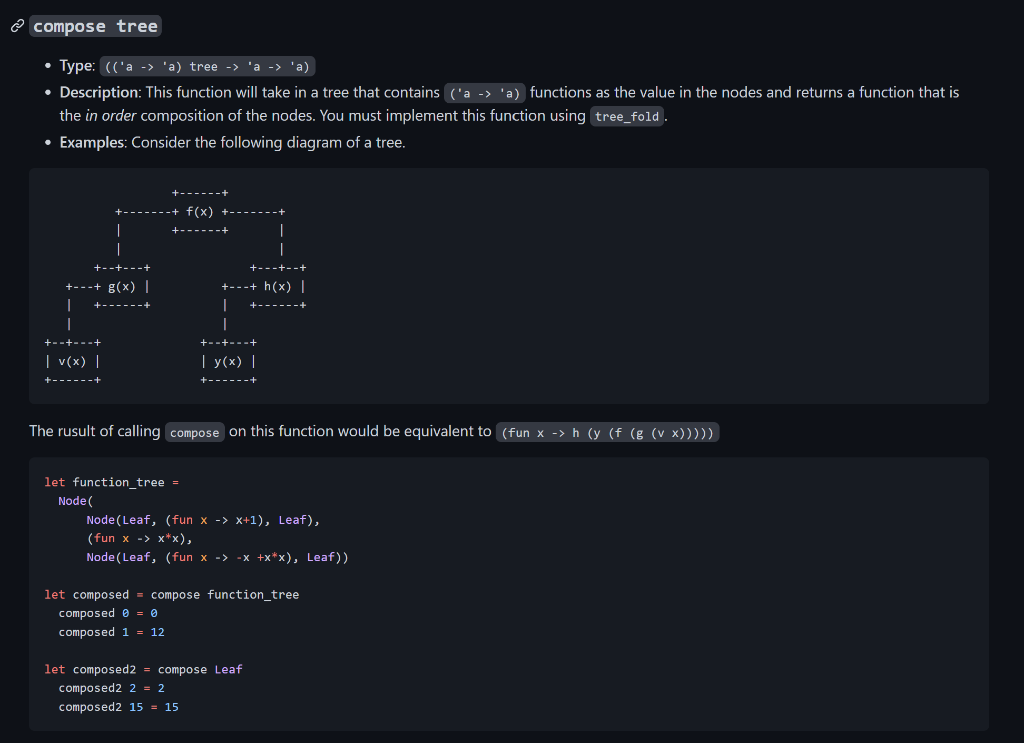
Given the tree_fold (fold_tree) function, please code a composed function as described in the image above.

The compose function takes in a tree that has Nodes with a left node and right node (that can be a leaf as well), and a value that is a function. The compose will then take those function in the order of top to down, left to right of the tree, and apply a function to another function in that order. For the given example above.

let function_tree = Node( Node(Leaf, (fun x -> x+1), Leaf), (fun x -> x*x), Node(Leaf, (fun x -> -x +x*x), Leaf))

(compose function_tree) 1 = (fun x -> x+1) -> (fun x -> x*x) -> (fun x -> -x +x*x), giving

1+1 = 2 -> 2*2 = 4 -> -4 + 4*4 = 12

and if the (compose tree) p is given a leaf as a parameter, it should just return that number instead as a leaf would not have any function.

For this code, please do not use recursion or any recursive helpers. You can use helpers as long as they are not recursive. You can also use any functions from the stdlib module and the List module libraries, but no other modules are allowed.

This is a hard program that I can't wrap my head around and I would appreciate it if you can answer it. Again, please follow the criteria I listed above, or else the code will be invalid.

If possible, also test that your word does what the example shows:

let function_tree = Node( Node(Leaf, (fun x -> x+1), Leaf), (fun x -> x*x), Node(Leaf, (fun x -> -x +x*x), Leaf)) let composed = compose function_tree composed 0 = 0 composed 1 = 12 let composed2 = compose Leaf composed2 2 = 2 composed2 15 = 15

I understand that this is a hard question, but please do help me with it.

type 'a tree = | Node of 'a tree *'a 'a 'a tree Leaf let rec fold_tree fbt= match t with \( \begin{array}{l}\mid \text { Leaf } \\ \mid \text { Node }(l, v, r) ightarrow \text { let res_l }=\text { fold_tree } f b l \text { in } \\ \quad \text { let res_r } r=\text { fold_tree } f b r \text { in } \\ \quad f \text { res_l } v \text { res_r }\end{array} \) compose tree - Type: (('a ' a ) tree 'a 'a) the in order composition of the nodes. You must implement this function using tree_fold. - Examples: Consider the following diagram of a tree. The rusult of calling compose on this function would be equivalent to ( fun xh(y(f(g(vx))))) let function_tree = Node ( Node(Leaf,(funx>x+1),Leaf))Node(Leaf,(funx>x+xx),Leaf))) \( \begin{aligned} \text { let composed } & =\text { compose function_tree } \\ \text { composed } 0 & =0 \\ \text { composed } 1 & =12 \\ \text { let composed2 } & =\text { compose Leaf } \\ \text { composed2 } 2 & =2 \\ \text { composed2 } 15 & =15\end{aligned} \)