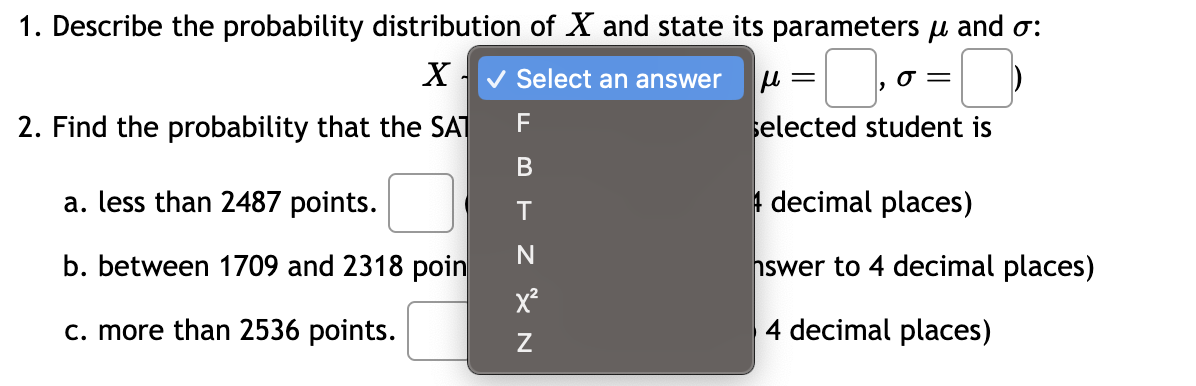
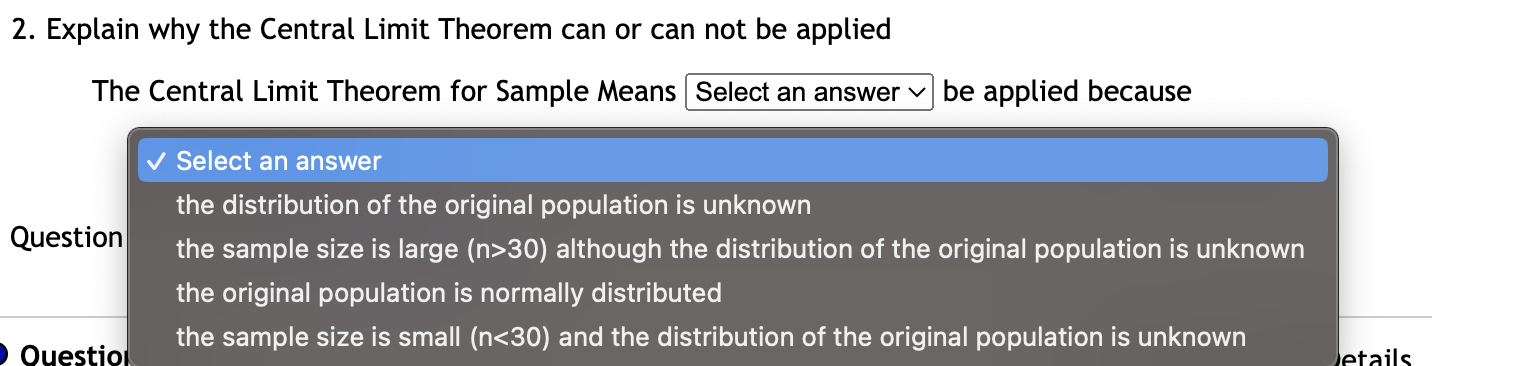
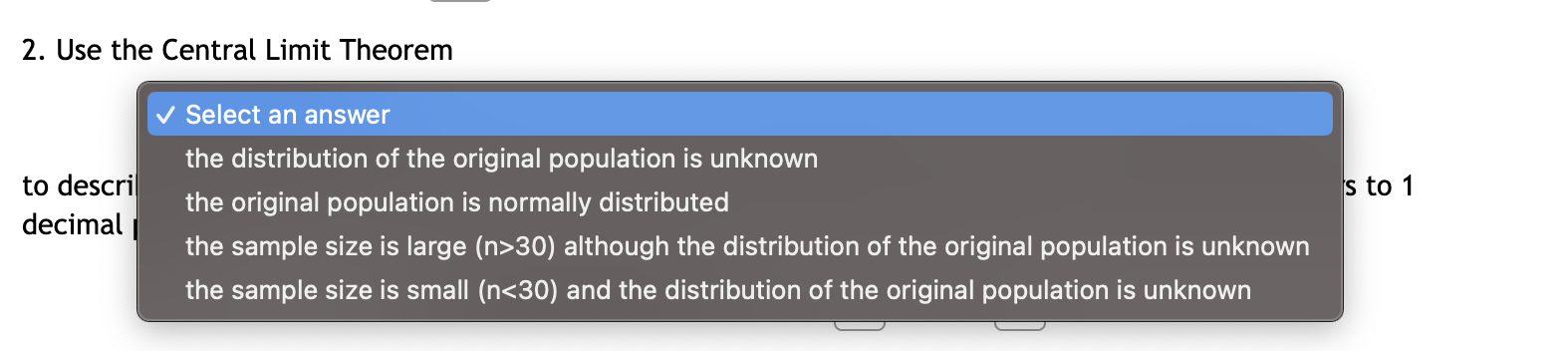
\fa probability density curve that (1) extends indefinitely in both directions, approaching, but never touching, the horizontal axis; (2) symmetric about 0; (3) as the number of degrees of freedom becomes larger, it increasingly looks like the standard normal curve v| a curve that (1) is always on or above the horizontal axis; (2) has the total area between itself and the horizontal axis equal to 1 a probability density curve that (1) starts at 0 on the horizontal axis and extends indefinitely to the right, approaching, but never touching, the horizontal axis; (2) is right skewed; (3) as the number of degrees of freedom becomes larger, it increasingly looks like a normal curve a probability density curve that (1) starts at 0 on the horizontal axis and extends indefinitely to the right, approaching, but never touching, the horizontal axis; (2) is right skewed; (3) possess the reciprocal property a random variable whose probability density function is portrayed as a horizontal line 1/(b-a) above the horizontal axis over the interval fromatob For the standard normal variable Z , find the probability P(Z 0.07): P(T > 0.07) = (Round the answer to 4 decimal places) Find to.6 for T distribution with 77 degrees of freedom. to.6 (Round the answer to 3 decimal places)For a normal variable X ~ N(u = 87.7,0 = 16.4), find the probability P(X 30) although the distribution of the original population is unknown the original population is normally distributed the sample size is small (n10 and n(1-p)>10 Suppose that the outstanding credit card balance of a randomly selected young man has an unknown distribution with a mean of 650 dollars and a standard deviation of 143.9 dollars. Let X be the outstanding credit card balance for a randomly selected young man and let X be the average outstanding credit card balance for a random sample of size 40. 1. Describe the probability distribution of X and state its parameters y and o X ~[Selectananswer~| (n=| Lo =| ) and find the probability that the outstanding credit card balance for a randomly selected young man is less than 738 dollars. (Round the answer to 4 decimal places) 2. Use the Central Limit Theorem Select an answer v to describe the probability distribution of X and state its parameters Kx and ox: (Round the answers to 1 decimal place) X ~|[Selectananswerv| (px = ,ox=| ) and find the probability that the average outstanding credit card balance for a sample of 40 randomly selected young men is less than 621 dollars. (Round the answer to 4 decimal places) 2. Use the Central Limit Theorem v Select an answer the distribution of the original population is unknown to descri to 1 . the original population is normally distributed decimal the sample size is large (n>30) although the distribution of the original population is unknown the sample size is small (n