Question: f(a) Solve the initialvalue problem 9 =_ help 6W) (b) Solve the initialvalue problem @_ di 9 =_ help (formulas) _3t9 y(0) = 3 (a)
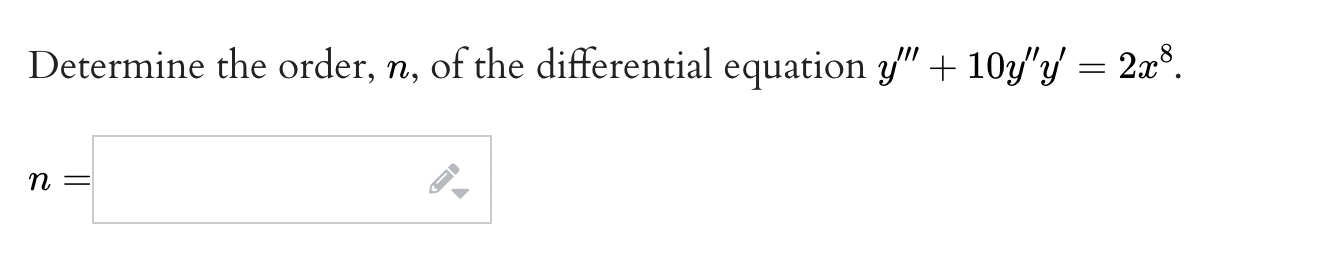



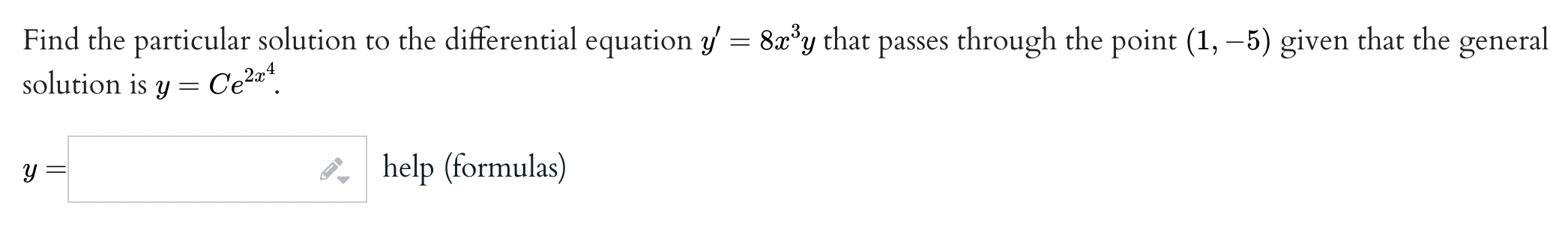
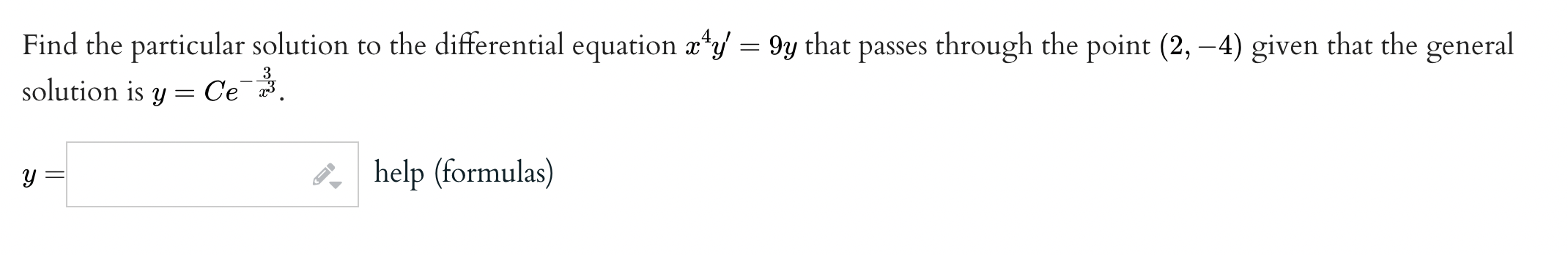
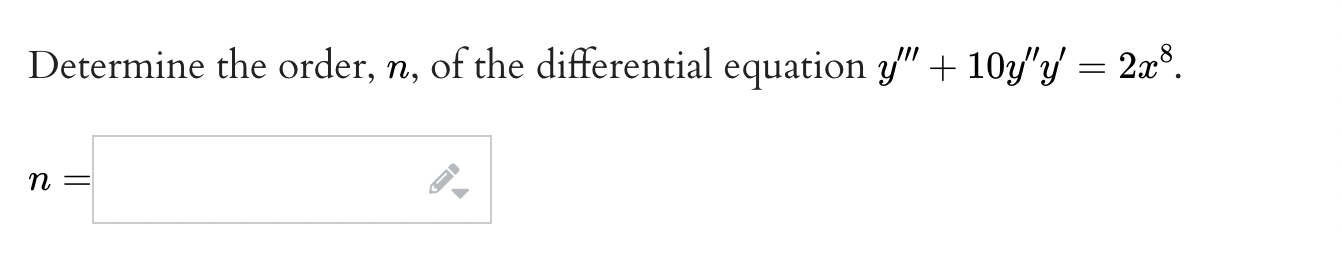



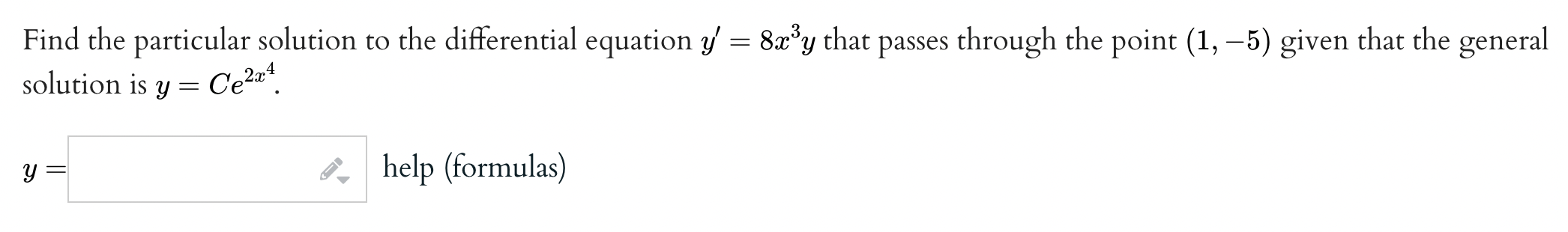
![y; help (formulas) Find the particular solution to the differential equation 1:43]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6666492d32697_4376666492d0ed32.jpg)
\f(a) Solve the initialvalue problem 9 =_ help 6W\") (b) Solve the initialvalue problem @_ di 9 =_ help (formulas) _3t9 y(0) = 3 (a) Solve the initialvalue problem = 2.5, y(0) = 3 y =_ help (formulas) (b) Solve the initialvalue problem _ di v =_ help (formulas) 2.5, y(0) = 1.5 (a) Solve the initialvalue problem. % = e'gt, yo = 12 y(t) = i. help (formulas) (b) The function y(t) either equals 86 or equals 6 at some point, but not both. For What value oft does this happen? at t = i, help (numbers) Find the particular solution to the differential equation 3/ = 8:333; that passes through the point (1, 5) given that the general . . 4 solution is y = Ce\" . y = y; help (formulas) Find the particular solution to the differential equation 1:43] = 9y that passes through the point (2, 4) given that the general 3 solution is y = (Ye3'. y = y; help (formulas)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


