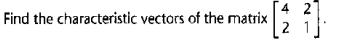
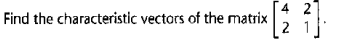
\fAnswer. - 1 2 To find the characteristic root, we have the characteristic equation 2 1- r =1 -5r =0. So, we find characteristic roots m, = 5 and ry =0. As r, > 0 and re 2 0, the characteristic root test shows that the matrix is positive semi-definite. For r, - 5, we have 12 - 0, 80 2) - 2c.. Upon normalization, the first characteristic vector is +1 For r2 - 0, we have (2 7) (2) - 0, 80 21 - $72. Upon normalization, the second characteristic vector is vi