Question: ffFor f(x) = +x-2 (x+2 ) does the Mean Value Theorem apply on the interval [0, 2] and why? The Mean Value Theorem does not
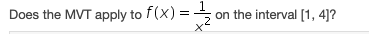
![apply on the interval [0, 2] and why? The Mean Value Theorem](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/11/67318fe635fca_35067318fe61756b.jpg)

![[0, 2]. O The Mean Value Theorem applies because f(x) is continuous](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/11/67318fe6c3856_35067318fe6a35cc.jpg)
![on [0, 2]. O The Mean Value Theorem applies because, f(x) is](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/11/67318fe70cba9_35067318fe6f009d.jpg)
![differentiable on the closed interval [0, 2]. O The Mean Value Theorem](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/11/67318fe74923a_35167318fe737d91.jpg)

![[0, 2].For f(x) = x3 - 2x + 1, find all the](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/11/67318fe7f25c8_35167318fe7df1fc.jpg)
\f\fFor f(x) = +x-2 (x+2 ) does the Mean Value Theorem apply on the interval [0, 2] and why? The Mean Value Theorem does not apply because f(x) is not continuous on the closed interval [0, 2]. O The Mean Value Theorem applies because f(x) is continuous on [0, 2]. O The Mean Value Theorem applies because, f(x) is differentiable on the closed interval [0, 2]. O The Mean Value Theorem does not apply because f(x) is not differentiable on the closed interval [0, 2].For f(x) = x3 - 2x + 1, find all the values of c on the interval [0, 2] that satisfy the Mean Value Theorem.Jon received his math grade for algebra. His class average over 10 tests is 89. Can you use the MVT to show that Jon must have received an 89 on one of the 10 tests?Theorem. For f (x) = - 1/x + 2 find all the values of c on the interval [2, 7] that satisfy the Mean Value O G= -4.25 C= -4.75 O c = 4.25 O c = 4.75For f X = X + 2 find all the values of c on the interval [0, 1] that satisfy the Mean Value Theorem. C= .778 O c= .5 O c = 0.4492 c= -0.5\f
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


