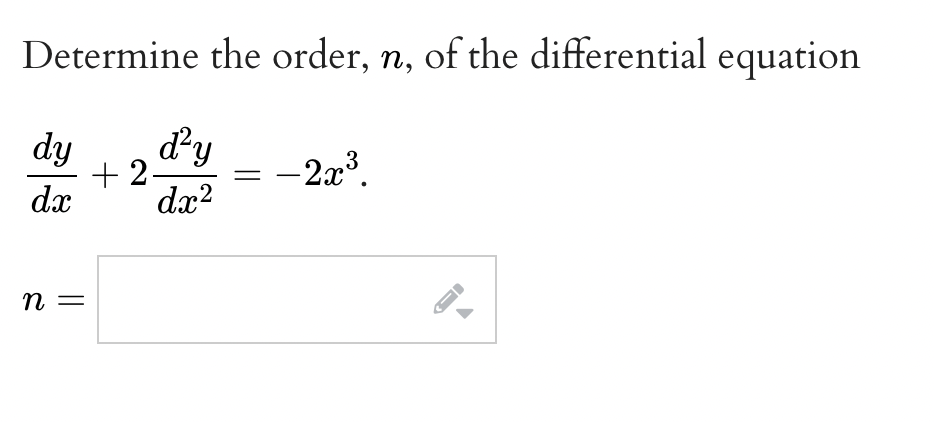
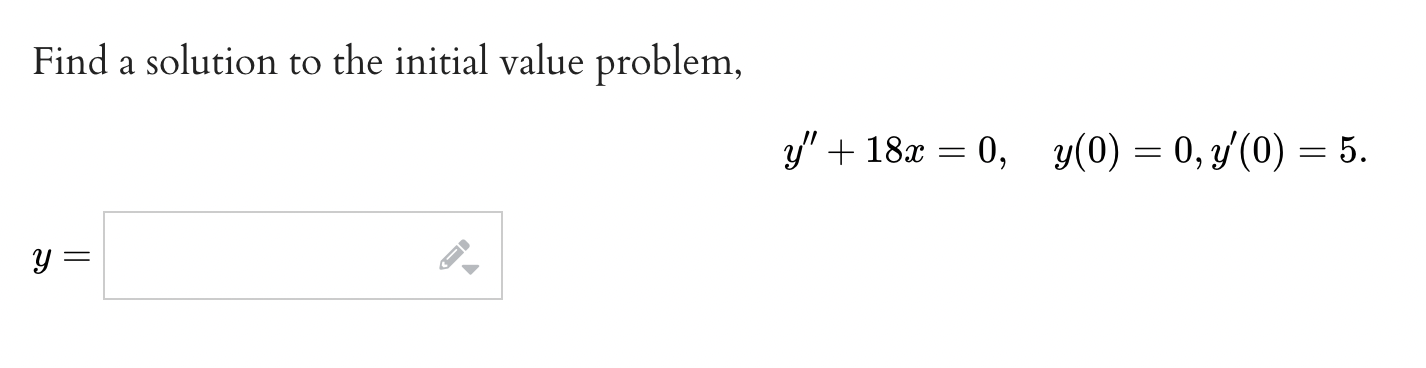
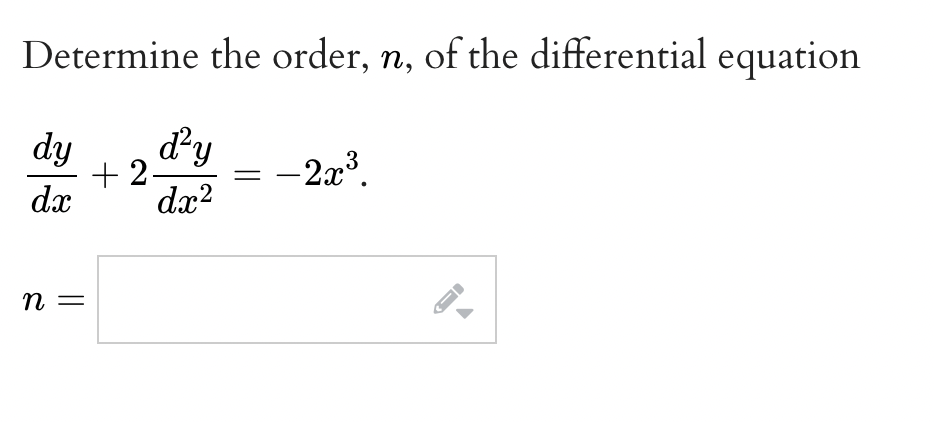
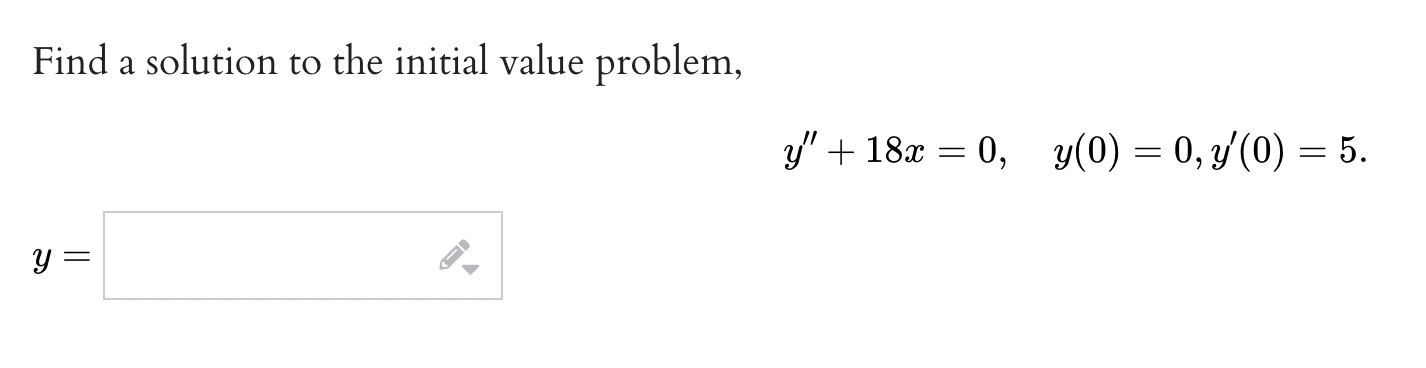
\fFor the differential equation y" + 4y = 0, a general solution is of the form y = C1 sin 2x + C2 cos 2x, where C1 and C2 are arbitrary constants. Applying the initial conditions y(0) = 2 and y'(0) = 10, find the specific solution. y =For the differential equation y\" + 43/ + 133/ = 0, a general solution is of the form y = e_2$(Cl sin 3m + 02 cos 32:), Where Cl and 02 are arbitrary constants. Applying the initial conditions y(0) = 2 and y'(0) = 1, nd the specic solution. 3;: f. \fFind a solution to the initial value problem, 3343/ + 4:333; = 96$, y(1) = 1 + 96. [Hint Interpret the lefthand side of the equation as the derivative of the product of two functions.] 9 = f