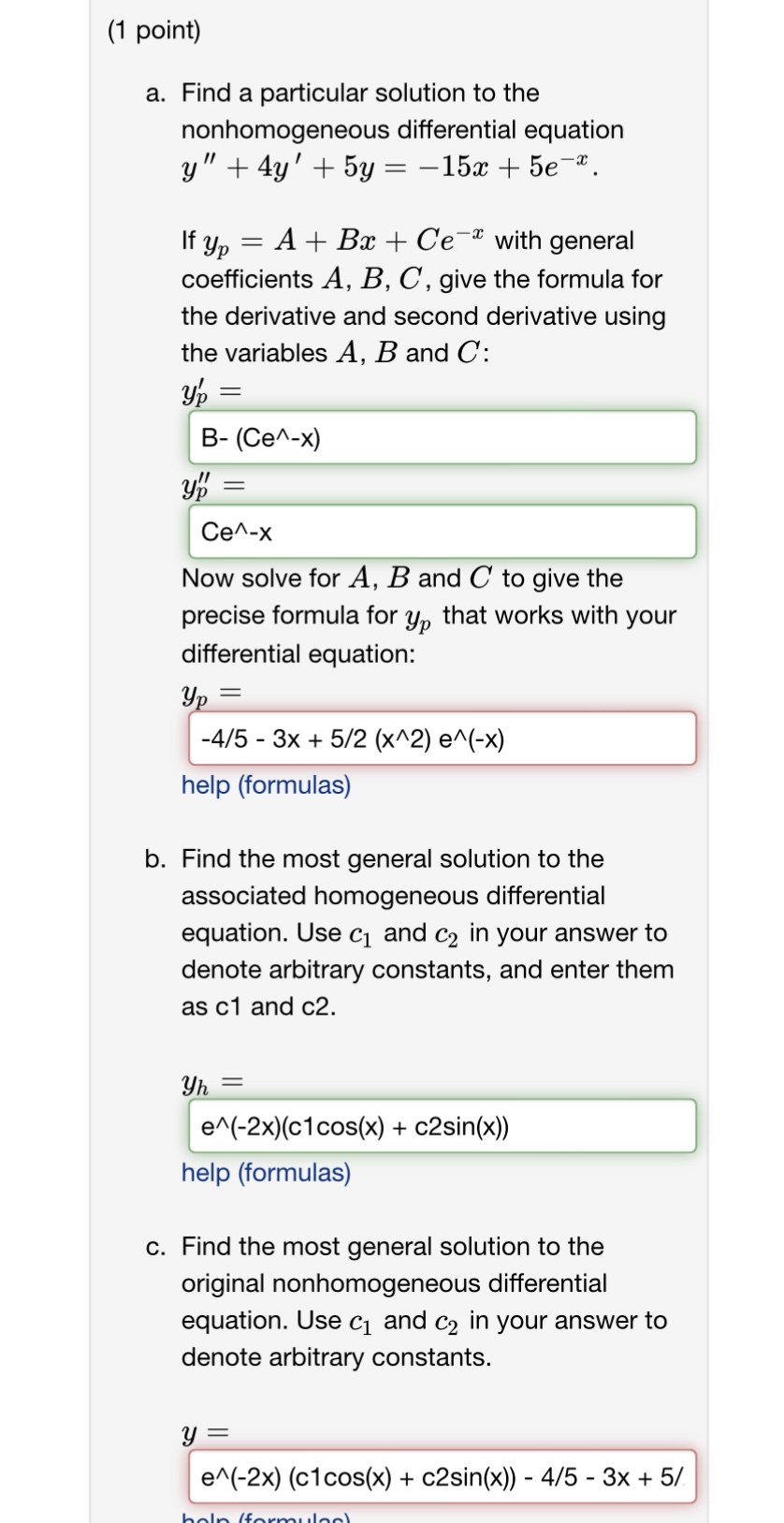
(1 point) Find a particular solution to y" + 16y = 8 sin (4t). Up(1 point) a. Find a particular solution to the nonhomogeneous differential equation y" + 4y' + 5y =-15x + 5e-*. If yp = A + Ba + Ce- with general coefficients A, B, C, give the formula for the derivative and second derivative using the variables A, B and C: Up = B- (Ce^-x) yp = Ce^-x Now solve for A, B and C to give the precise formula for yp that works with your differential equation: yp = -4/5 - 3x + 5/2 (x^2) e^(-x) help (formulas) b. Find the most general solution to the associated homogeneous differential equation. Use c1 and C2 in your answer to denote arbitrary constants, and enter them as c1 and c2. yh = e^(-2x)(c1cos(x) + c2sin(x)) help (formulas) c. Find the most general solution to the original nonhomogeneous differential equation. Use c1 and C2 in your answer to denote arbitrary constants. y = e^(-2x) (c1cos(x) + c2sin(x)) - 4/5 - 3x + 5/