\ Finally, we analyse

f(x)

near gaps in its domain.\ e) Find the point(s)

x=a

where

f(a)

is undefined.\ FORMATTING: List these points. If there are two or more such points, you must separate them by semi-colons (?. Since we are asking for exact values, your answers may involve the logarithm function ).\ Answer:\ f) For each of the values of (Y) that you have found in (e), find the left-hand and right-hand limits of

f

as

x

approaches

a

. Then answer the questions below.\ FORMATTING: If there are two or more points, separate them with semi-colons (?. Since we are asking for exact values, your answers may involve the logarithmic function

ln()

. You must use the notation of scientific calculators So

2x

is written

2^(**)x

, and so on. If there aren't any points, write empty.\ For which point(s)

a

do we have

\\\\lim_(x->a^(-))f(x)=+\\\\infty

? Answer:\ For which point(s)

a

do we have

\\\\lim_(x->a^(-))f(x)=-\\\\infty

? Answer:\ For which point(s) a do we have

\\\\lim_(x->a^(+))f(x)=+\\\\infty

? Answer:\ For which point(s) a do we have

\\\\lim_(x->a^(+))f(x)=-\\\\infty

? Answer:

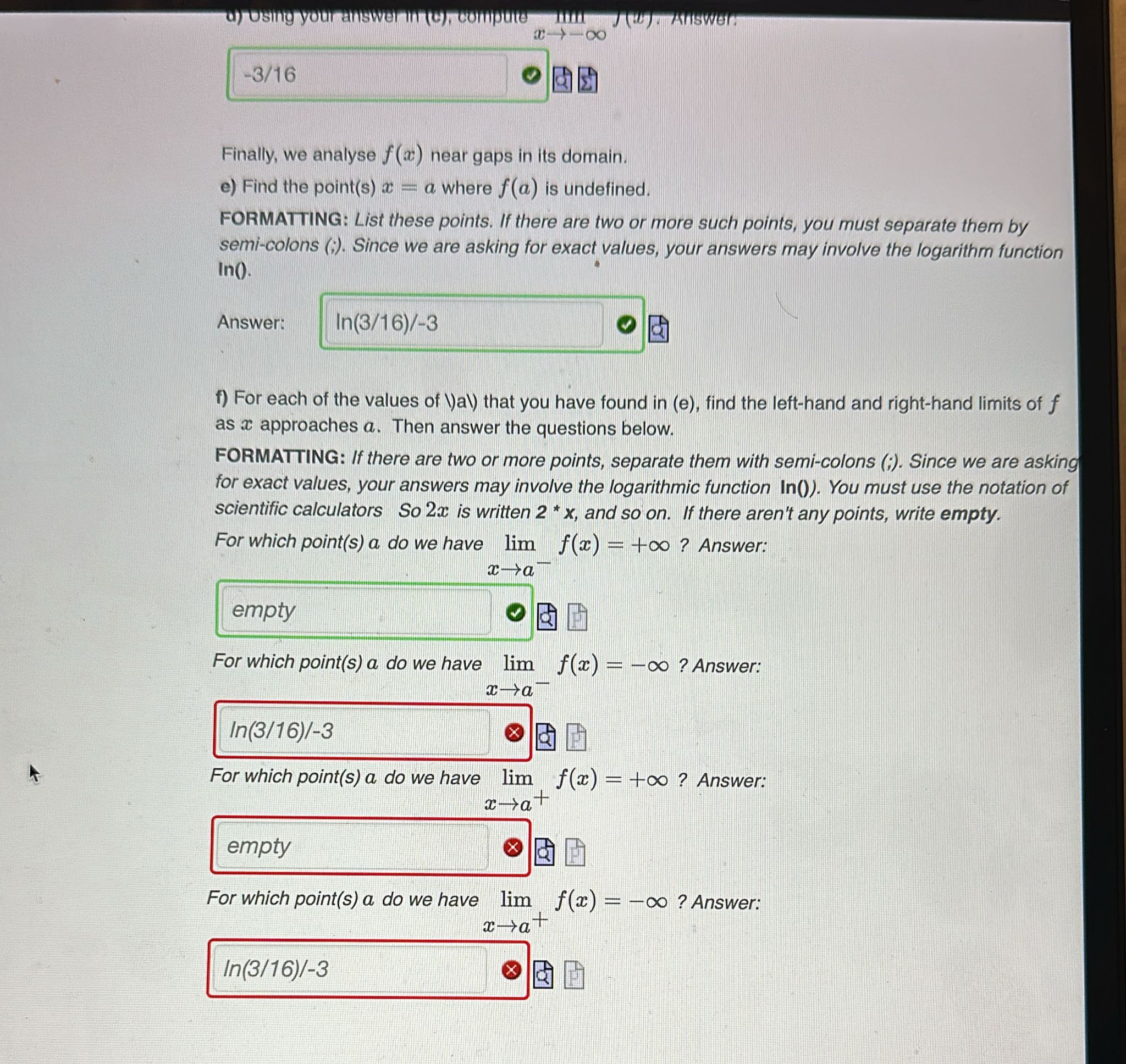
Finally, we analyse f(x) near gaps in its domain. e) Find the point(s) x=a where f(a) is undefined. FORMATTING: List these points. If there are two or more such points, you must separate them by semi-colons (;). Since we are asking for exact values, your answers may involve the logarithm function ln(). Answer: f) For each of the values of (Y)a) that you have found in (e), find the left-hand and right-hand limits of f as x approaches a. Then answer the questions below. FORMATTING: If there are two or more points, separate them with semi-colons (;). Since we are asking for exact values, your answers may involve the logarithmic function In()). You must use the notation of scientific calculators So 2x is written 2 * x, and so on. If there aren't any points, write empty. For which point(s) a do we have limxaf(x)=+ ? Answer: For which point(s) a do we have limxaf(x)= ? Answer: 2] For which point(s) a do we have limxa+f(x)=+ ? Answer: For which point(s) a do we have limxa+f(x)=