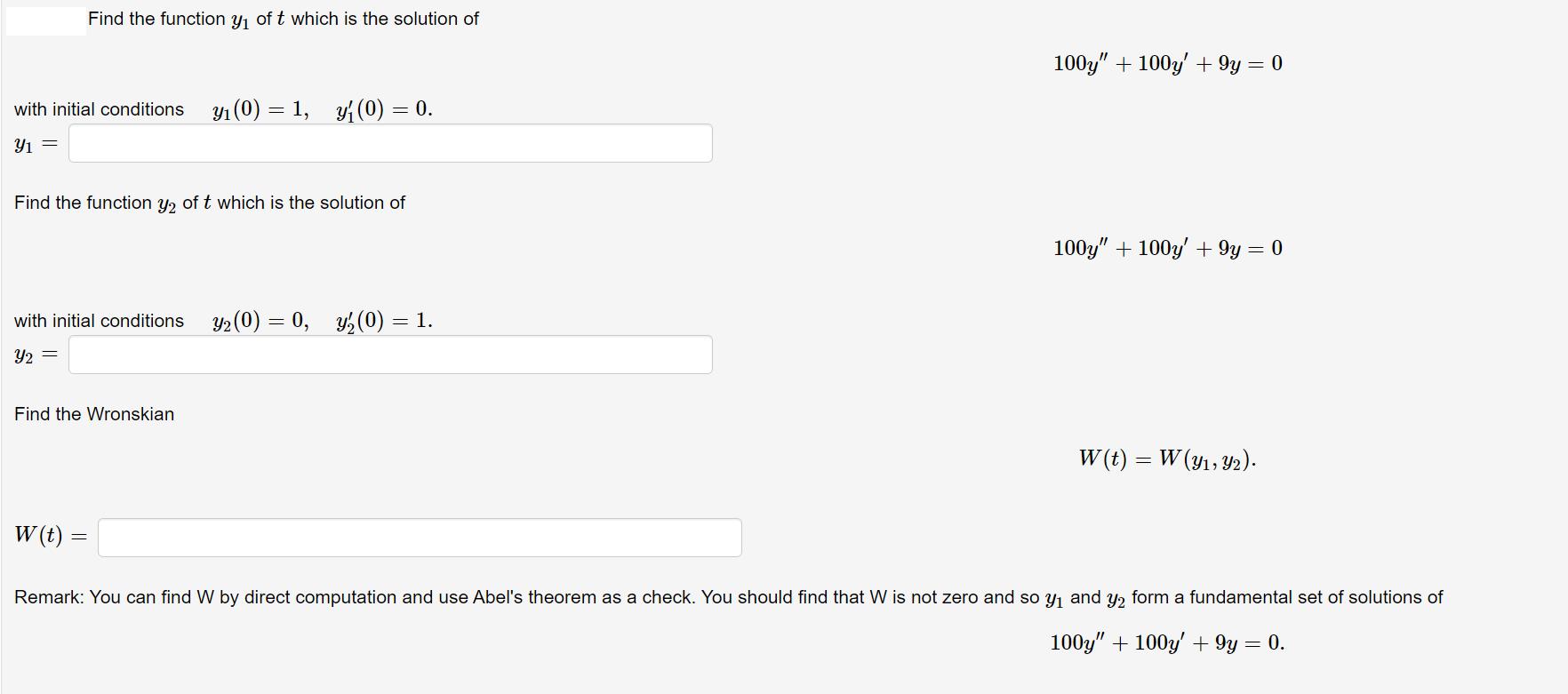
Find the function y of t which is the solution of with initial conditions y (0) = 1, y (0) = 0. Y1 = Find the function y2 of t which is the solution of with initial conditions y2 (0) = 0, y (0) = 1. Y2 = Find the Wronskian 100y" + 100y' + 9y = 0 100y" + 100y' + 9y = 0 W(t) = W (y, Y2). W (t) Remark: You can find W by direct computation and use Abel's theorem as a check. You should find that W is not zero and so y and y form a fundamental set of solutions of 100y" + 100y' + 9y = 0.