Question: Find the geodesic equations and geodesic for spherical polar coordinates? Show that every point of R3 is isotropic for the metric ds = (x)-2(dx1)2

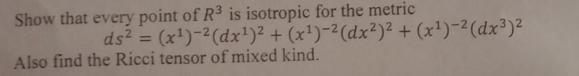
Find the geodesic equations and geodesic for spherical polar coordinates? Show that every point of R3 is isotropic for the metric ds = (x)-2(dx1)2

+ (x1)-2(dx) + (x1)-(dx)2 Also find the Ricci tensor of mixed kind.

Find the geodesic equations and geodesic for spherical polar coordinates? Show that every point of R3 is isotropic for the metric ds = (x)-2(dx1)2 + (x1)-2(dx) + (x1)-(dx)2 Also find the Ricci tensor of mixed kind. Question 3: (a) Define the followings (15 Marks) (i) Invariant (ii) Tensor (iii) Riemannian curvature (iv) Affine Tensor (v) Arc length (vi) Cartesian Tensor (6) (b) Prove the second Bianchi's identity? (9)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

4. The transformation equations between Cartesian and spherical polar coordinates involve the equation r=vx+y+= 0 = arccos- Vx'+ y'+= = arctan Calculate: ax 5. The transformation equations between...

4. The transformation equations between Cartesian and spherical polar coordinates involve the equation r=vx+y'+?' 0 = arccos Vx'+ y' +2 = arctan Calculate: ax 5. The transformation equations between...

1. The transformation equations between Cartesian and spherical polar coordinates involve the equation r= \\x+ y+2 0 = arccos Vx+ y'+z = arctan ~ X Calculate: 2. The transformation equations between...

Consider the surface of a zero-pressure star, which implodes along a time like geodesic r = R(t) in the Schwarzschild spacetime of its exterior. Analyze that implosion using Schwarzschild coordinates...

.. Help me please 1. Transform (using the coordinate system provided below) the following functions accordingly: Z Y X a. from cartesian to spherical polar coordinates 3x + y - 4z = 12 b. from...

3 problems to solve in jupyter python. it relates to programming and maths. DO NOT USE any file compression method. While the tasks below mention magnetic fields and particle orbits, you do not need...

Consider a small satellite in a noncircular orbit about a spherical body with much larger mass M, for which the external gravitational field is Schwarzschild. The satellite will follow a timelike...

In n + 1 space dimensions we have Cartesian coordinates a = (1, n+1) and spherical polar coordinates (r. 2), where :-) (...) are n angles. They are related by ra]. The integral over all space can be...

Please solve with steps. P.S. The general formulas for divergence and curl in curvilinear coordinates are attached for reference. 2. Consider the spherical polar coordinates (r, 0, 4) with unit...

Determine (a) the temperature at the 16 equally spaced points shown in the accompanying sketch to an accuracy of three significant figures and (b) the rate of heat flow per meter thickness. Assume...

What is the profit from the sale on 15.01.2023 according to the Last In First Out (LIFO) method? Stock at the Beginning of the Period: 2.000 kg 10 /kg 05.01.2023 Buying Goods: 5.000 kg 12 /kg...

South Carolina Corporation has one temporary difference at the end of 2 0 2 0 that will reverse and cause taxable amounts of $ 5 5 , 0 0 0 in 2 0 2 1 , $ 6 0 , 0 0 0 in 2 0 2 2 , and $ 7 5 , 0 0 0 in...

Control charts have many applications in operations. Define and provide an example of at least 3 applications where control charts would be beneficial to an operations manager?

5. Starting with a motive you may have for acting the way you do in a particular situation: a) What purpose did you seek to achieve? b) Which aspects of your past and your surroundings influenced...

3. (Constructing a metaphor about something can be done by comparing it to something else by using the word is. For instance, Communication is a bridge between people.

1. The first party (the sender) may dispute the validity of the interpretation, or 2. He/she can accept the interpretation.